Sección : Tests no paramétricos
Previo : Test de Kolmogorov-Smirnov
Siguiente : Test de chi-cuadrado de contingencia

Test de ajuste de chi-cuadrado

El test de chi-cuadrado es únicamente para las leyes discretas, pero se puede utilizar también para muestras continuas agrupadas en clases. El caso típico es, como siempre, el de una muestra $(X_1,\ldots,X_n)$ de una ley desconocida. Las clases, denotadas $c_1,\ldots,c_r$, son una partición del conjunto de los valores posibles. La hipótesis a comprobar tiene que ver con las probabilidades de las clases, para las cuales se toman valores teóricos $P_0(c_1)\ldots,P_0(c_r)$.

$${\cal H}_0\;:\; \mathbb {P}[ X_i\in c_k] = P_0(c_k)\,,\;\forall k=1,\ldots,r\;.$$

Bajo la hipótesis ${\cal H}_0$, la distribución empírica de la muestra sobre las clases debe estar cerca de la distribución teórica. La distribución empírica es la de las frecuencias de la muestra en las clases:

$$\widehat{P}(c_k) = \frac{1}{n}\sum_{i=1}^n \mathbb {I}_{c_k}(X_i)\;.$$

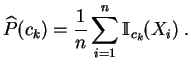
Se mide el ajuste de la distribución empírica a la distribución teórica por la distancia de chi-cuadrado.

Definición 2.3   Se llama distancia de chi-cuadrado de $\widehat{P}$ con respecto a $P_0$, y se denota por $D_{\chi^2}(P_0,\widehat{P})$, al valor:

$$D_{\chi^2}(P_0,\widehat{P}) = \sum_{h=1}^r \frac{(P_0(c_h)-\widehat{P}(c_h))^2}{P_0(c_h)}\;.$$

La ''distancia'' de chi-cuadrado es por tanto una media ponderada de las diferencias cuadráticas entre los valores de $P_0$ y $\widehat{P}$. No es una distancia en el sentido usual del término, pues ni siquiera es simétrica. La ley de probabilidad de $D_{\chi^2}(P_0,\widehat{P})$ no tiene una expresión explícita en general. Se emplea entonces el siguiente resultado.

Teorema 2.4   Bajo la hipótesis ${\cal H}_0$ la ley de la variable aleatoria $nD_{\chi^2}(P_0,\widehat{P})$ converge, cuando $n$ tiende a infinito, a la ley de chi-cuadrado de parámetro $r\!-\!1$.

Si la hipótesis ${\cal H}_0$ es falsa, entonces la variable $nD_{\chi^2}(P_0,\widehat{P})$ tiende a infinito. Por tanto aplicaremos un test unilateral a la derecha (rechazo de los valores muy grandes).
 

El ejemplo clásico del test es la experiencia de Mendel. En los guisantes, el carácter del color esta codificado por un gen que toma dos formas de alelo $C$ y $c$, correspondientes a los colores amarillo y verde respectivamente. El amarillo es dominante, el verde recesivo. La forma lisa o arrugada es llevada por otro gen con dos alelos $R$ (dominante) y $r$ (recesivo). Si se cruzan dos individuos cuyo genotipo es $CcRr$, se pueden obtener $16$ genotipos equiprobables. Los descendientes serán amarillos y lisos en $9$ casos de los $16$, amarillos y arrugados en $3$ de los $16$, verdes y lisos en $3$ de los $16$, verdes y arrugados en $1$ caso de los $16$. En sus experiencias Mendel obtuvo los siguientes resultados.

	Amarillo	Amarillo	Verde	Verde
	Liso	Arrugado	Liso	Arrugado
Casos	315	101	108	32
$\widehat{P}(c_h)$	0.567	0.182	0.194	0.058
$P_0(c_h)$	9/16	3/16	3/16	1/16

El valor que toma el estadígrafo $nD_{\chi^2}(P_0,\widehat{P})$ es de $0.47$. Según el teorema 2.4, la región de rechazo debe ser calculada con respecto a la ley de chi-cuadrado ${\cal X}^2(3)$. Por ejemplo, para un umbral $0.05$, deberíamos rechazar los valores superiores a
$Q_{{\cal X}^2(3)}(0.95) = 7.81$. El p-valor de $0.47$ es $1-F_{{\cal X}^2(3)}(0.47) = 0.925$. El resultado es por tanto completamente compatible con ${\cal H}_0$, de hecho es un poco ``demasiado'' compatible: son muchos los que piensan que Mendel pudo haber arreglado los resultados de sus experimentos para que estos coincidieran tan bien con su teoría !
 

El ejemplo que damos a continuación tiene que ver con $10000$ familias de $4$ hijos para las cuales se conoce el número de varones, entre 0 y $4$.

El modelo más simple que podemos proponer es que los nacimientos son independientes y los dos sexos son equiprobables. Por tanto la hipótesis nula es que la ley del número de varones para una familia de $4$ hijos sigue la ley binomial ${\cal B}(4,0.5)$. Las frecuencias, observadas y teóricas, son las siguientes.

Varones	0	1	2	3	4
$\widehat{P}(c_h)$	0.0572	0.2329	0.3758	0.2632	0.0709
$P_0(c_h)$	1/16	4/16	6/16	4/16	1/16

El valor que toma el estadígrafo $nD_{\chi^2}(P_0,\widehat{P})$ es de $34.47$. Según el teorema 2.4, la región de rechazo debe ser calculada con respecto a la ley chi-cuadrado de parámetro $5\!-\!1=4$. Por ejemplo para un umbral de $0.05$, deberíamos rechazar los valores superiores a $Q_{{\cal X}^2(4)}(0.95) = 9.49$. El p-valor de $34.47$ es $1-F_{{\cal X}^2(4)}(34.47) = 5.97\,10^{-7}$. Podemos, por tanto, rechazar la hipótesis ${\cal H}_0$.
 

El teorema 2.4 es un resultado asintótico. Para poder usarlo, el orden del tamaño de las muestras debe ser al menos de las centenas. Además la aproximación que describe es menos buena cuando las probabilidades de las clases son débiles. Como regla empírica, se exige que los efectivos teóricos $nP(c_k)$ de cada clase sean al menos iguales a $5$. Para alcanzar este objetivo a veces hay que recurrir al reagrupamiento de las clases : se forman nuevas clases uniendo varias de las iniciales, y se suman las frecuencias empíricas y las probabilidades teóricas de las clases agrupadas.
 

El test de chi-cuadrado se emplea con frecuencia para hacer un test de la bondad de ajuste a una familia particular de leyes que dependen de uno o más parámetros. En este caso, se debe estimar el parámetro a partir de los datos. El teorema 2.4 no es ya del todo válido. Si se han estimado $h$ parámetros por el método de máximo de verosimilitud, a partir de las frecuencias de las diferentes clases, se debe remplazar la ley ${\cal X}^2(r\!-\!1)$ por la ley ${\cal X}^2(r\!-\!1\!-\!h)$.

Retomemos el ejemplo del número de varones en una familia de $4$ hijos, pero esta vez para probar la hipótesis nula:

$${\cal H}_0\;:\;$$el número de varones sigue una ley binomial $${\cal B}(4,p)\;.$$

El parámetro $p$ es desconocido y debe ser estimado. El estimador de máximo de verosimilitud (el cual maximiza la probabilidad de los datos observados) es en este caso la proporción total de varones entre los $40000$ niños. Encontramos:

$$\widehat{p} = 0.5144\;.$$

Ahora aplicamos el test, pero con la distribución teórica calculada teniendo en cuenta el valor estimado del parámetro: la ley ${\cal B}(4,\widehat{p})$.

Varones	0	1	2	3	4
$\widehat{P}(c_h)$	0.0572	0.2329	0.3758	0.2632	0.0709
$P_0(c_h)$	0.0556	0.2356	0.3744	0.2644	0.0700

El valor que toma el estadígrafo $nD_{\chi^2}(P_0,\widehat{P})$ es ahora de $0.9883$. Debe ser comparado con los valores de la ley chi-cuadrado de parámetro $5-1-1=3$. El p-valor de $0.9883$ es $1-F_{{\cal X}^2(3)}(0.9883) = 0.8041$, lo cual muestra que el resultado es perfectamente compatible con la hipótesis ${\cal H}_0$.

Al comparar los resultados de los dos tests precedentes, se puede aceptar la idea que los nacimientos son independientes, pero la proporción de los varones es significativamente superior a $0.5$.
 

Con frecuencia hay que estimar parámetros a partir de datos no agrupados, o por otro método diferente al de máximo de verosimilitud. En ese caso no se dispone de un resultado teórico claro. El valor límite a partir del cual se debe rechazar la hipótesis ${\cal H}_0$ al umbral $\alpha$ está comprendido entre $Q_{{\cal X}^2(r-1-h)}(1-\alpha)$ y $Q_{{\cal X}^2(r-1)}(1-\alpha)$. En la práctica, después de haber calculado el valor $t$ que toma $nD_{\chi^2}(P_0,\widehat{P})$ teniendo en cuenta los $h$ parámetros estimados, es prudente tomar la siguiente actitud:

$\bullet$

rechazar ${\cal H}_0$ si $t>Q_{{\cal X}^2(r-1)}(1-\alpha)$,

$\bullet$

no rechazar ${\cal H}_0$ si $t<Q_{{\cal X}^2(r-1-h)}(1-\alpha)$,

$\bullet$

no llegar a una conclusión si $Q_{{\cal X}^2(r-1-h)}(1-\alpha)<t<Q_{{\cal X}^2(r-1)}(1-\alpha)$.

Sección : Tests no paramétricos
Previo : Test de Kolmogorov-Smirnov
Siguiente : Test de chi-cuadrado de contingencia