Test de Kolmogorov-Smirnov

El test de Kolmogorov-Smirnov es un test de ajuste a una ley continua que tiene en cuenta el conjunto de los cuantiles, en contraposición al test local del parrafo anterior. El caso típico sigue siendo que se tiene una muestra $(X_1,\ldots,X_n)$ de una ley

desconocida. La hipótesis nula es:

$\displaystyle {\cal H}_0\;:\;$ la ley

tiene por función de distribución a

$\displaystyle \;,$

donde

es la función de distribución de una ley continua dada. La idea es la siguiente: si la hipótesis ${\cal H}_0$ es correcta, entonces la función de distribución empírica $\widehat{F}$ de la muestra debe parecerse a la función

. La función de distribución empírica es la función que va de $\mathbb {R}$ en $[0\,,1]$ , y que toma los valores:

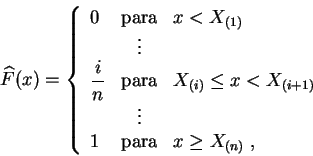
$\begin{displaymath} \widehat{F}(x) = \left\{ \begin{array}{lcl} 0 &\mbox{para... ...ts&\\ 1&\mbox{para}&x\geq X_{(n)}\;, \end{array} \right. \end{displaymath}$

Medimos el ajuste de la función de distribución empírica a la función

por la distancia de Kolmogorov-Smirnov, la cual es la distancia asociada a la norma uniforme entre funciones de distribución. Para calcularla basta evaluar la diferencia entre $\widehat{F}$ y

en los puntos $X_{(i)}$ .

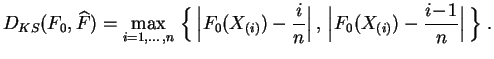
$\displaystyle D_{KS}(F_0,\widehat{F}) = \max_{i=1,\ldots,n}\, \Big\{\,\Big\ver... ...}\Big\vert\,,\, \Big\vert F_0(X_{(i)})-\frac{i\!-\!1}{n}\Big\vert\,\Big\}\;.$

Bajo la hipótesis ${\cal H}_0$ , la ley del estadígrafo $D_{KS}(F_0,\widehat{F})$ no depende de

, porque los valores que toma

en los

son variables aleatorias de ley ${\cal U}(0,1)$ . Pero la función de distribución de $D_{KS}(F_0,\widehat{F})$ no tiene una expresión explícita simple y debe ser calculada numéricamente. Para muestras de tamaño suficientemente grande, se emplea el siguiente resultado asintótico:

Proposición 2.2 Bajo la hipótesis ${\cal H}_0$ , se tiene, para todo $t\geq 0$ :

$\displaystyle \lim_{n\rightarrow\infty} \mathbb {P}_{{\cal H}_0}[\,\sqrt{n}D_{... ...0,\widehat{F})\leq t\,] = 1-2\sum_{k=1}^{+\infty}(-1)^{k+1}\exp(-2k^2t^2)\;.$

La serie converge muy rápidamente. En la práctica, para $t\geq 1$ , la suma de los tres primeros términos ya da una aproximación excelente. Si la hipótesis ${\cal H}_0$ es falsa, $\sqrt{n}D_{KS}(F_0,\widehat{F})$ tiende a $+\infty$ con

. El test es por tanto necesariamente unilateral a la derecha (rechazo de valores muy grandes). Supongamos que la distancia $D_{KS}(F_0,\widehat{F})$ toma el valor

para una muestra de tamaño

. El estadígrafo $\sqrt{n}D_{KS}(F_0,\widehat{F})$ vale

. El p-valor correspondiente es:

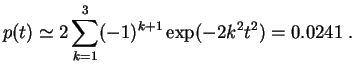
$\displaystyle p(t) \simeq 2\sum_{k=1}^{3}(-1)^{k+1}\exp(-2k^2t^2)=0.0241\;.$

El test de Kolmogorov-Smirnov se extiende a la comparación de dos funciones de distribución empíricas y permite entonces poner a prueba la hipótesis de si dos muestras salieron de la misma ley. Se pueden utilizar muchos otros tests de ajuste, como los de Stephens, Anderson-Darling y Cramer-von Mises.