Un caso particular del test de chi-cuadrado, que permite hacer un test
sobre la independencia de dos carácteres estadísticos, lleva el
nombre de
test
de chi-cuadrado de contingencia. Los dos
carácteres, observados en una misma población, son ![]() e
e ![]() , el
tamaño de la muestra es
, el
tamaño de la muestra es ![]() . Las modalidades o clases de
. Las modalidades o clases de ![]() se
denotan
se
denotan
![]() , las de
, las de ![]() por
por
![]() .
También vamos a denotar :
.
También vamos a denotar :
Estos valores se representan en una tabla de doble entrada conocida como tabla de contingencia.
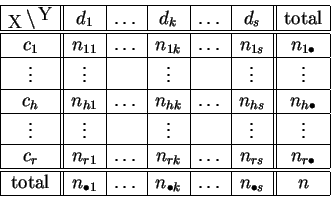
Cada fila y cada columna corresponden a una submuestra particular.
La fila de índice ![]() es la distribución en las clases
es la distribución en las clases
![]() de los individuos para los cuales el carácter
de los individuos para los cuales el carácter
![]() toma el valor
toma el valor ![]() . La columna de índice
. La columna de índice ![]() es la
distribución en las clases
es la
distribución en las clases
![]() de los individuos
para los cuales el carácter
de los individuos
para los cuales el carácter ![]() toma el valor
toma el valor ![]() . Dividiendo
las filas y las columnas por su suma, se obtienen frecuencias
condicionales para cada una de las distribuciones empíricas.
Para
. Dividiendo
las filas y las columnas por su suma, se obtienen frecuencias
condicionales para cada una de las distribuciones empíricas.
Para
![]() y
y
![]() , las denotaremos por:
, las denotaremos por:
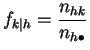 y
y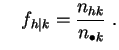
Estas distribuciones empíricas condicionales se llaman los
perfiles fila y los perfiles columna.
Para el modelo probabilista, las observaciones provienen de una
muestra
![]() de una ley
bidimensional. La hipótesis a comprobar es que los dos
marginales de esta ley son independientes. Si este es el caso, los
perfiles fila diferirán poco de la distribución empírica de
de una ley
bidimensional. La hipótesis a comprobar es que los dos
marginales de esta ley son independientes. Si este es el caso, los
perfiles fila diferirán poco de la distribución empírica de
![]() y los perfiles columna de la de
y los perfiles columna de la de ![]() :
:
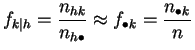 y
y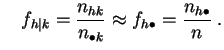
Es equivalente a decir que las frecuencias conjuntas deben estar cerca de los productos de las frecuencias marginales.
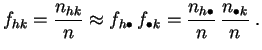
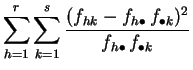 |
|||
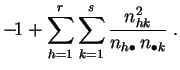 |
Demostración :
La primera expresión es la aplicación directa de la
definición 2.3. Para obtener la segunda
desarrollamos el cuadrado.
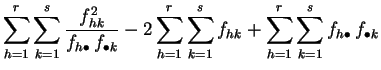 |
|||
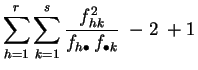 |
|||
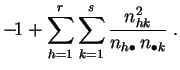 |
Por lo dicho anteriormente, para ![]() suficientemente grande,
podemos aproximar la ley de
suficientemente grande,
podemos aproximar la ley de
![]() por la ley de
chi-cuadrado cuyo parámetro es el número de clases menos
por la ley de
chi-cuadrado cuyo parámetro es el número de clases menos ![]() ,
restando además el número de parámetros estimados a partir
de los datos agrupados en clases. Aquí, son las frecuencias
marginales las que han sido estimadas. Hay
,
restando además el número de parámetros estimados a partir
de los datos agrupados en clases. Aquí, son las frecuencias
marginales las que han sido estimadas. Hay ![]() para el
carácter
para el
carácter ![]() y
y ![]() para el carácter
para el carácter ![]() (la última es
el complemento a
(la última es
el complemento a ![]() de la suma de las otras). El parámetro de
la ley chi-cuadrado será por tanto:
de la suma de las otras). El parámetro de
la ley chi-cuadrado será por tanto:
Vamos a presentar un ejemplo de dos carácteres binarios, que
tienen que ver con enfermos, para los cuales se ha observado si
tienen o no una tendencia al suicidio (carácter ![]() ). Las
enfermedades han sido clasificadas como ''psicosis'' y
''neurosis'' (carácter
). Las
enfermedades han sido clasificadas como ''psicosis'' y
''neurosis'' (carácter ![]() ). Se quiere saber si existe una
dependencia entre las tendencias al suicidio y la clasificiación
de los enfermos. Supongamos que la
tabla
de contingencia observada
es:
). Se quiere saber si existe una
dependencia entre las tendencias al suicidio y la clasificiación
de los enfermos. Supongamos que la
tabla
de contingencia observada
es:
La distancia de chi-cuadrado de contingencia, calculada a partir
de esta tabla es de ![]() . El valor tomado por el estadígrafo
. El valor tomado por el estadígrafo
![]() es
es ![]() , el cual debemos comparar con la ley
, el cual debemos comparar con la ley
![]() . El p-valor es de:
. El p-valor es de:
Rechazamos la hipótesis nula y concluimos que hay una dependencia entre la tendencia al suicidio y la clasificación de las enfermedades.
El test no precisa el sentido de esta dependencia. Para
describirla hay que comparar las proporciones de los suicidas
entre los neuróticos (![]() ) y entre los sicóticos
(
) y entre los sicóticos
(![]() ). El
test de
proporciones formaliza esta comparación.
). El
test de
proporciones formaliza esta comparación.