Sección : Intervalos de confianza
Previo : Muestras gaussianas
Siguiente : Normalidad asintótica

Modelo lineal

Las muestras gaussianas son utilizadas frecuentemente para modelar los errores en los modelos de regresión. Estos modelos buscan explicar un carácter $Y$ (considerado como aleatorio) por carácteres (deterministas) $(x^{(1)},\ldots,x^{(k)})$. Se escoge una función de regresión $f$, que depende en general de varios parámetros desconocidos, y se escriben las variables aleatorias $Y_i$ de la forma:

$$Y_i = f(x^{(1)}_i,\ldots,x^{(k)}_i)+E_i\;,$$

donde $(E_1,\ldots,E_n)$ es una $n$-tupla de variables aleatorias independientes y con una misma ley. Los parámetros desconocidos de $f$ serán estimados por el método de los mínimos cuadrados, minimizando el error cuadrático:

$$EQ(f) = \frac{1}{n} \sum_{i=1}^n (Y_i-f(x^{(1)}_i,\ldots,x^{(k)}_i))^2\;.$$

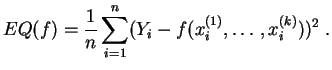
En el caso en que la función $f$ es afín y $(E_1,\ldots,E_n)$ es una muestra gaussiana, se puede determinar explícitamente la ley de los estimadores de mínimos cuadrados y de ella deducir intervalos de confianza.

Nosotros solamente consideraremos la regresión lineal simple:

$$Y_i = a x_i + b +E_i\;,$$

donde $E_i$ es una muestra de la ley normal ${\cal N}(0,\sigma^2)$. En otras palabras, suponemos que las $Y_i$ son variables aleatorias gaussianas independientes, de esperanzas $ax_i+b$ diferentes, pero con la misma varianza $\sigma^2$. El modelo tiene 3 parámetros desconocidos, $a$, $b$ y $\sigma^2$. Estimamos $a$ y $b$ minimizando el error cuadrático:

$$EQ(a,b) = \frac{1}{n} \sum_{i=1}^n (Y_i-ax_i-b)^2\;.$$

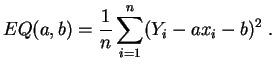
Obtenemos así (ver la sección 2.3) los estimadores de mínimos cuadrados:

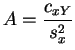$$A = \frac{c_{xY}}{s_x^2}$$   y$$\quad B = \overline{Y} - A\overline{x}\;.$$

El error cuadrático minimal es:

$$EQ(A,B) = S_Y^2(1-r_{xY}^2)\;.$$

Estas tres variables aleatorias son estimadores consistentes de $a$, $b$ y $\sigma^2$ respectivamente. Los dos primeros son insesgados. La esperanza de $EQ(A,B)$ es $(n-2)\sigma^2/n$, por tanto es asintóticamente insesgado. Se obtiene un estimador insesgado y consistente de $\sigma^2$ tomando:

$$V=\frac{n}{n-2} EQ(A,B)\;.$$

La predicción es el primer objetivo de un modelo probabilista. En el caso de la regresión lineal, si un nuevo individuo es examinado, con un valor observado $x_*$ para el carácter $x$, el modelo conlleva que el valor $Y_*$ del carácter explicado para este individuo es una variable aleatoria de ley normal ${\cal N}(ax_*+b,\sigma^2)$. Los parámetros de esta ley tendrán por estimadores a $Ax_*+B$ y $EQ(A,B)$ respectivamente.

El siguiente teorema permite calcular las leyes de estos estimadores y por tanto intervalos de confianza. Lo podemos considerar como una extensión del teorema 3.3.

Teorema 3.4   Con las notaciones precedentes:

1. $${\sqrt{\frac{ns_x^2}{\sigma^2}}(A-a)}$$ sigue la ley normal ${\cal N}(0,1)$.
2. $${\sqrt{\frac{ns_x^2}{V}}(A-a)}$$ sigue la ley de Student ${\cal T}(n-2)$.
3. $${\sqrt{\frac{ns_x^2}{\sigma^2(s_x^2+(x^*-\overline{x})^2)}} (Ax^*+B-ax^*-b)}$$ sigue la ley normal ${\cal N}(0,1)$.
4. $${\sqrt{\frac{ns_x^2}{V(s_x^2+(x^*-\overline{x})^2)}} (Ax^*+B-ax^*-b)}$$ sigue la ley de Student ${\cal T}(n-2)$.
5. $${(n-2)\frac{V}{\sigma^2}}$$ sigue la ley de chi-cuadrado ${\cal X}^2(n\!-\!2)$.

Estos resultados se emplean de la misma manera que el teorema 3.3 para deducir intervalos de confianza. Denotamos $[-z_\alpha , z_\alpha]$, $[-t_\alpha,t_\alpha]$ y $[u_\alpha,v_\alpha]$ los intervalos de dispersión optimales de nivel $1\!-\!\alpha$ para las leyes ${\cal N}(0,1)$, ${\cal T}(n-2)$ y ${\cal X}^2(n-2)$ respectivamente. Los intervalos de confianza de nivel $1\!-\!\alpha$ correspondientes a los diferentes incisos del teorema 3.4 son:

1. Intervalo de confianza para $a$, si se conoce $\sigma^2$.
   $$\left[\,A-z_\alpha\sqrt{\frac{\sigma^2}{ns_x^2}}\;,\; A+z_\alpha\sqrt{\frac{\sigma^2}{ns_x^2}}\,\right]\;.$$

2. Intervalo de confianza para $a$, si no se conoce $\sigma^2$.
   $$\left[\,A-t_\alpha\sqrt{\frac{V}{ns_x^2}}\;,\; A+t_\alpha\sqrt{\frac{V}{ns_x^2}}\,\right]\;.$$

3. Intervalo de confianza para $ax_*+b$, si se conoce $\sigma^2$.
   $$\left[\,Ax_*+B-z_\alpha \sqrt{\frac{\sigma^2(s_x^2+(x^*-\overlin... ...alpha\sqrt{\frac{\sigma^2(s_x^2+(x^*-\overline{x})^2)}{ns_x^2}} \,\right]\;.$$

4. Intervalo de confianza para $ax_*+b$, si no se conoce $\sigma^2$.
   $$\left[\,Ax_*+B-t_\alpha \sqrt{\frac{V(s_x^2+(x^*-\overline{x})^2... ...*+B+t_\alpha\sqrt{\frac{V(s_x^2+(x^*-\overline{x})^2)}{ns_x^2}} \,\right]\;.$$

5. Intervalo de confianza para $\sigma^2$.
   $$\left[\,(n-2)\frac{V}{v_\alpha}\;,\;(n-2)\frac{V}{u_\alpha}\,\right]\;.$$

Si se quiere predecir el valor de $Y_*=ax_*+b+E_*$ para un nuevo individuo, habrá que tener en cuenta no solamente el error cometido al estimar el valor de $ax_*+b$ sino también el de la varianza $\sigma^2$ de $E_*$. Esto aumenta la longitud del intervalo. Veamos el intervalo de predicción de $Y_*$, siempre al nivel $1\!-\!\alpha$, cuando no se conoce $\sigma^2$ (estimada por $V$).

$$\left[\,Ax_*\!+\!B-t_\alpha \sqrt{\frac{V((n\!+\!1)s_x^2+(x^*\!-... ...sqrt{\frac{V((n\!+\!1)s_x^2+(x^*\!-\!\overline{x})^2)}{ns_x^2}} \,\right]\,.$$

Como ejemplo, consideremos la estatura en centímetros ($x_i$) y el peso en kilogramos ($y_i$) de $10$ niños de $6$ años.

Niño	1	2	3	4	5	6	7	8	9	10
Estatura	121	123	108	118	111	109	114	103	110	115
Peso	25	22	19	24	19	18	20	15	20	21

Las características numéricas toman los valores siguientes:

$$\begin{array}{\vert cccccccc\vert} \hline \overline{x}&\o... ....3&34.76&7.61&0.9&0.42&-\!27.38&1.44\\ \hline \end{array}$$

Hacer una regresión lineal quiere decir que pensamos que el peso debe aumentar, en general, proporcionalmente a la estatura. La recta de regresión lineal es un modelo de predicción. Para un niño de estatura dada, daremos un intervalo de peso, considerado como ``normal'', la normalidad se define en referencia al modelo y a los datos. Estos son los intervalos de predicción de nivel $0.95$ para diferentes estaturas.

estatura	intervalo de peso
100	$[10.82\,,\,18.67]$
110	$[15.65\,,\,22.25]$
120	$[19.72\,,\,26.61]$
130	$[23.09\,,\,31.66]$

Los intervalos de predicción son menos precisos según que el tamaño de la muestra inicial sea pequeño y que el valor de $x_*$ esté más lejos de $\overline{x}$ (ver el gráfico 5).

Los resultados precedentes se extienden a las regresiones lineales múltiples. Las expresiones explícitas de los intervalos de confianza son demasiado complicadas para reproducirlas aquí, pero están programadas en todos los logiciales de cálculo estadístico.

Sección : Intervalos de confianza
Previo : Muestras gaussianas
Siguiente : Normalidad asintótica