Hasta ahora el único modelo
probabilista que hemos considerado para datos observados, suponía
que estos eran realizaciones de variables independientes de una
misma ley. Esto equivale a decir que los individuos en los cuales
se tomaron los datos son intercambiables y que las diferencias
observadas entre ellos son imputables solamente al azar. En
numerosas situaciones, se busca explicar estas diferencias,
es decir, atribuirlas a los efectos de otros carácteres medidos en
los mismos individuos. La modelación probabilista considerará que
la medición a explicar, realizada en un individuo dado, es
una variable aleatoria cuya ley depende de los valores observados,
en ese individuo, de los carácteres explicativos, considerados
como deterministas. Si ![]() denota la variable aleatoria asociada
al individuo
denota la variable aleatoria asociada
al individuo ![]() y
y
![]() son los valores
que toman, para ese individuo, los carácteres explicativos
son los valores
que toman, para ese individuo, los carácteres explicativos
![]() , se separará el efecto determinista y
el efecto aleatorio por un modelo del tipo:
, se separará el efecto determinista y
el efecto aleatorio por un modelo del tipo:
donde
![]() es una
es una ![]() -tupla de variables aleatorias
independientes con una misma ley. Hablamos entonces de un
modelo de regresión. La función
-tupla de variables aleatorias
independientes con una misma ley. Hablamos entonces de un
modelo de regresión. La función ![]() depende de uno o varios
parámetros desconocidos, que hay que estimar. Para esto se busca
minimizar el
error cuadrático definido por:
depende de uno o varios
parámetros desconocidos, que hay que estimar. Para esto se busca
minimizar el
error cuadrático definido por:
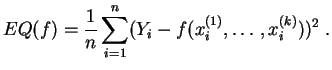
En algunos casos clásicos, sabemos
resolver explícitamente este problema de minimización y la
solución de estos está implementada en los logiciales de cálculo
estadístico. Cuando una solución explícita es imposible,
recurrimos a algoritmos de minimización, como por ejemplo el
algoritmo del gradiente.
El caso más elemental es el de la
regresión lineal simple,
donde hay un único carácter explicativo y la función ![]() es afín:
es afín:
El error cuadrático está dado por:
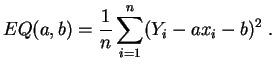
Los valores de ![]() y
y ![]() que minimizan el error cuadrático se
expresan en función de las medias, varianzas y covarianzas
empíricas de
que minimizan el error cuadrático se
expresan en función de las medias, varianzas y covarianzas
empíricas de ![]() y de
y de ![]() . Denotamos:
. Denotamos:
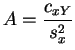 y
y
Las variables aleatorias ![]() y
y ![]() son los estimadores de
mínimos cuadrados de los parámetros
son los estimadores de
mínimos cuadrados de los parámetros ![]() y
y ![]() .
.
En un problema de ajuste, podemos emplear los estimadores de
mínimos cuadrados para estimar los parámetros de algunas leyes.
Vamos a tratar, como ejemplo, las
leyes
normales y las
leyes de
Weibull.
Leyes normales:
Sea
![]() una muestra de tamaño
una muestra de tamaño
![]() de la ley normal
de la ley normal
![]() , donde los
parámetros
, donde los
parámetros ![]() y
y ![]() son desconocidos. Para
son desconocidos. Para
![]() , denotemos por
, denotemos por ![]() el
estadígrafo de
orden (son los valores
el
estadígrafo de
orden (son los valores ![]() ordenados del
menor al mayor). Si la hipótesis de normalidad es válida, entonces
ordenados del
menor al mayor). Si la hipótesis de normalidad es válida, entonces
![]() debe estar cerca del cuantil
debe estar cerca del cuantil
![]() de la ley
de la ley
![]() .
Recordemos que si una variable aleatoria
.
Recordemos que si una variable aleatoria ![]() sigue la ley
sigue la ley
![]() , entonces
, entonces
![]() sigue la ley
sigue la ley
![]() . Esto implica que para todo
. Esto implica que para todo
![]() :
:
Denotemos
![]() los valores
de la función cuantil de la ley
los valores
de la función cuantil de la ley
![]() en los puntos
en los puntos ![]() . Si la hipótesis de normalidad se
verifica, los puntos de coordenadas
. Si la hipótesis de normalidad se
verifica, los puntos de coordenadas
![]() deberían estar
cerca de la recta de ecuación
deberían estar
cerca de la recta de ecuación
![]() . Los estimadores de
mínimos cuadrados
. Los estimadores de
mínimos cuadrados ![]() y
y ![]() para la
regresión lineal simple de los
para la
regresión lineal simple de los
![]() con respecto a los
con respecto a los ![]() son por tanto estimadores de
son por tanto estimadores de
![]() y
y ![]() respectivamente.
respectivamente.
Leyes de Weibull:
La función cuantil de la ley de Weibull
![]() está dada por:
está dada por:
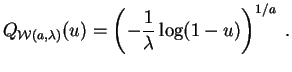
Sea
![]() una muestra de la ley
una muestra de la ley
![]() , de parámetros
, de parámetros ![]() y
y ![]() desconocidos. Para
desconocidos. Para
![]() , el
estadígrafo de orden
, el
estadígrafo de orden ![]() debe estar
cerca del cuantil
debe estar
cerca del cuantil
![]() :
:
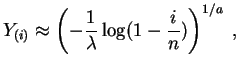
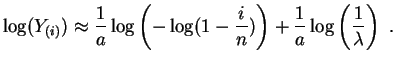
Denotemos
![]() y
y
![]() . Los
puntos
. Los
puntos
![]() deberían estar cerca de la recta de ecuación
deberían estar cerca de la recta de ecuación
![]() . Los estimadores de mínimos
cuadrados
. Los estimadores de mínimos
cuadrados ![]() y
y ![]() para la
regresión lineal de los
para la
regresión lineal de los ![]() con
respecto a los
con
respecto a los ![]() son estimadores de
son estimadores de ![]() y
y
![]() respectivamente. Por tanto
respectivamente. Por tanto ![]() y
y
![]() son estimadores de
son estimadores de ![]() y
y ![]() respectivamente.
respectivamente.