Sección : Tests no paramétricos
Previo : Test de chi-cuadrado de contingencia
Siguiente : Tests de Wilcoxon y Mann-Whitney

Test de proporciones

En este parrafo consideramos el problema de un test para la independencia de dos carácteres binarios, indicadores de dos eventos distintos. Es una situación que se encuentra en la medicina cada vez que se plantea el problema de una detección terapéutica. Llamemos $E$ (por enfermedad) al primer evento y $S$ (por síntoma) al segundo. El síntoma puede ser una tasa elevada de una cierta sustancia o la reacción positiva a un test de detección, como un test de alcoholemia. En cada individuo de una población de tamaño $n$, se observan la presencia o la ausencia de la enfermedad y del síntoma. Tenemos entonces los $4$ resultados posibles siguientes :

$\bullet$

$n_{ES}$ : número de individuos enfermos y que presentan el síntoma,

$\bullet$

$n_{E\overline{S}}$ : número de individuos enfermos que no presentan el síntoma,

$\bullet$

$n_{\overline{E}S}$ : número de individuos no enfermos que presentan el síntoma,

$\bullet$

$n_{\overline{E}\,\overline{S}}$ : número de individuos no enfermos que no presentan el síntoma.

El problema es extraer de estos datos una base para un diagnóstico : ¿con qué certeza podemos anunciar a una persona que está enferma, si se ha encontrado el síntoma en ella? La hipótesis nula es:

$${\cal H}_0\;:\;$$los eventos $E$ y $S$ son independientes.$$$$

El test de chi-cuadrado, visto en el parrafo anterior, es uno de los medios de comprobar ${\cal H}_0$. Tiene el inconveniente de no distinguir una tendencia positiva (la presencia del síntoma inclina a favor de la presencia de la enfermedad) de una dependencia negativa. También se utiliza el cociente de apuestas, o relación de proporciones (odds-ratio en inglés). La proporción o apuesta (en el sentido de los jugadores) de un evento es el cociente entre la probabilidad del evento y la de su complementario. Esta ``apuesta'' se puede calcular para la enfermedad en los individuos que tienen el síntoma ( $P[E\,\vert\,S]/P[\overline{E}\,\vert\,S]$) y en los que no lo tienen ( $P[E\,\vert\,\overline{S}]/P[\overline{E}\,\vert\,\overline{S}]$). La proporción teórica de las apuestas es el cociente de estas dos cantidades:

$$OR = \frac{P[E\,\vert\,S]/P[\overline{E}\,\vert\,S]}{ P[E\,\vert... ...erline{E}\cap\overline{S}]}{ P[\overline{E}\cap S]\,P[E\cap\overline{S}]}\;.$$

La proporción entre apuestas vale $1$ si la enfermedad y el síntoma son independientes, es mayor que $1$ si la presencia del síntoma indica la presencia de la enfermedad. Cuando se han realizado observaciones en una muestra, podemos aproximar las probabilidades teóricas por las frecuencias experimentales. Esto nos lleva a la definición de la proporción empírica de las apuestas.

Definición 2.6   Se llama proporción empírica de las apuestas a:

$$\mathop{\widehat{OR}} = \frac{n_{ES}\, n_{\overline{E}\,\overline{S}} }{ n_{\overline{E}S}\,n_{E\overline{S}}}\;.$$

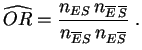
Cuando el denominador es cero, por convenio se reemplaza la definición de $\widehat{OR}$ por:

$$\widehat{OR} = \frac{(n_{ES}+0.5)\, (n_{\overline{E}\,\overline{S}}+0.5) }{ (n_{\overline{E}S}+0.5)\,(n_{E\overline{S}}+0.5)}\;.$$

 

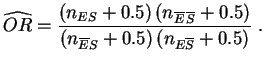
Ejemplo: Retomemos los datos del parrafo anterior.

	tendencia	sin tendencia	total
psicosis	20	180	200
neurosis	60	140	200
total	80	320	400

La apuesta (empírica) de las neurosis en los individuos que tienen tendencias suicidas es:

$$\frac{n_{ES} / n_S}{n_{\overline{E}S} / n_S} = \frac{60}{20}\;.$$

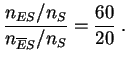
Para los que no tienen tendencias, la apuesta es:

$$\frac{n_{E\overline{S}} / n_{\overline{S}} }{ n_{\overline{E}\,\overline{S}} / n_{\overline{S}}} = \frac{140}{180}\;.$$

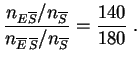
La proporción de apuestas empírica vale:

$$\widehat{OR} = \frac{60/20}{140/180} = 3.857\;.$$

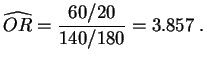
Hay una tendencia positiva entre las tendencias suicidas y las neurosis. La cuestión es saber si esta dependencia es significativa. Es difícil dar explícitamente la ley de probabilidad de la proporción de apuestas bajo la hipótesis ${\cal H}_0$, por una via que no sea la simulación. Para muestras grandes se emplea el siguiente resultado asintótico.

Teorema 2.7   Denotemos por $V$ a la variable aleatoria igual a la suma de los inversos de los cuatro coeficientes.

$$V = \frac{1}{n_{ES}}+\frac{1}{n_{\overline{E}S}} +\frac{1}{n_{E\overline{S}}}+\frac{1}{n_{\overline{E}\,\overline{S}}}\;.$$

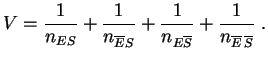
Bajo la hipótesis de independencia ${\cal H}_0$, la ley de la variable aleatoria:

$$T=\frac{\log(\widehat{OR})}{\sqrt{V}}$$

converge a la ley normal ${\cal N}(0,1)$.

En nuestro ejemplo el estadígrafo $T$ toma el valor $4.7918$. Su p-valor es:

$$1-F_{{\cal N}(0,1)}(4.7918) = 8.266\,10^{-7}\;.$$

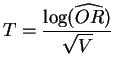
Podemos por tanto concluir que hay una dependencia positiva entre tendencias suicidas y neurosis.

Sección : Tests no paramétricos
Previo : Test de chi-cuadrado de contingencia
Siguiente : Tests de Wilcoxon y Mann-Whitney