Tests de Wilcoxon y Mann-Whitney

Retomemos el problema de hacer un test del efecto de un tratamiento sobre un carácter dado (por ejemplo la tasa de colesterol). Los valores de colesterol medidos a un grupo de control sin tratamiento corresponden a una primera muestra $(X_1,\ldots,X_{n_x})$ de la ley

. En otro grupo, con tratamiento, los valores medidos son los de una segunda muestra $(Y_1,\ldots,Y_{n_y})$ correspondientes a la ley

. Las dos leyes

son desconocidas. Si el tratamiento no tiene ningún efecto (hipótesis nula), las dos leyes son idénticas.

La idea del test de Wilcoxon es la siguiente: si unimos las dos muestras, y ponemos los valores en orden, la alternancia entre las

y las

debería ser bastante regular. Tendríamos dudas sobre ${\cal H}_0$ si los

eran en general más grandes que los

, o más pequeños, o más frecuentes en ciertos tramos de la sucesión de valores. Comenzamos por tanto por escribir los estadígrafos de orden de la muestra global (si hay valores iguales se escoge al azar una permutación de ellos) Se obtiene así una sucesión de los valores

mezclados. A continuación se calcula la suma de los rangos de los

, que denotamos por

(es el estadígrafo de Wilcoxon). Bajo la hipótesis ${\cal H}_0$ , la ley de

se calcula fácilmente: en una muestra de tamaño

hay

ordenes posibles. El número de formas posibles de distribuir a los

es $\binom{n_x+n_y}{n_x}$ , y son todos equiprobables. Por tanto para todo entero

entre $\binom{n_x}{2}$ y $\binom{n_x+n_y}{2}-\binom{n_y}{2}$ tenemos:

$\displaystyle \mathbb {P}_{{\cal H}_0}[\,W_x = m\,] = \frac{k_m}{\binom{n_x+n_y}{n_x}}\;,$

$\displaystyle 1\leq r_1<r_2<\cdots<r_{n_x}\leq n_x+n_y\;.$

Es fácil tabular numéricamente la ley de

para valores razonables de

. Para valores grandes, se dispone del siguiente resultado de aproximación normal:

Teorema 2.8 Bajo la hipótesis ${\cal H}_0$ , la ley de :

$\displaystyle \frac{W_x - n_x(n_x+n_y+1)/2}{\sqrt{n_xn_y(n_x+n_y+1)/12}}$

converge a la ley normal ${\cal N}(0,1)$ .

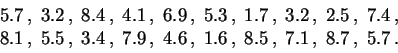
$\begin{displaymath} \begin{array}{c} 5.7\,,\;3.2\,,\;8.4\,,\;4.1\,,\;6.9\,,\; ... ...4.6\,,\; 1.6\,,\;8.5\,,\;7.1\,,\;8.7\,,\;5.7\,. \end{array} \end{displaymath}$

Este es el estadígrafo de orden de la muestra reagrupada de tamaño

(los valores

de la primera muestra están subrayados).

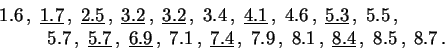
$\begin{displaymath} \begin{array}{c} 1.6\,,\;\underline{1.7}\,,\;\underline{2.... ...,,\;8.1\,,\; \underline{8.4}\,,\;8.5\,,\;8.7\,. \end{array} \end{displaymath}$

Los valores de la primera muestra tienen tendencia a ser más pequeños que los de la segunda muestra. Se quiere saber si esta tendencia es significativa, realizaremos por tanto un test unilateral a la izquierda (rechazo de un valor muy pequeño de

). El p-valor correspondiente es:

El test de Mann-Whitney se obtiene a partir de otro punto de vista, pero es equivalente al anterior. En el ejemplo presentado anteriormente, queríamos verificar que los valores de la primera muestra eran con mayor frecuencia más pequeños que los de la segunda muestra. Para esto podíamos haber contado el número de pares

para los cuales

(con una decisión aleatoria en caso de igualdad):

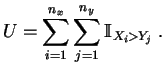
$\displaystyle U = \sum_{i=1}^{n_x}\sum_{j=1}^{n_y} \mathbb {I}_{X_i>Y_j}\;.$

Los dos tests son, por tanto, completamente equivalentes. En nuestro ejemplo, el estadígrafo

toma el valor :