Media empírica

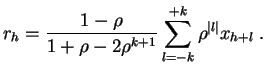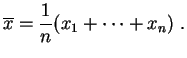
El estadígrafo más evidente que se puede calcular en una muestra numérica, aquella cuya interpretación es más intuitiva, es la media empírica.

Definición 1.1 La media empírica de una muestra es la suma de sus elementos dividida por el número de ellos. Si la muestra se denota por $(x_1,\ldots,x_n)$ , su media empírica es:

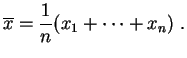
$\displaystyle \overline{x} = \frac{1}{n} (x_1+\cdots+x_n)\;.$

Por tanto la media es el centro de gravedad de los datos, dando el mismo peso a todos los individuos. Ella puede ser considerada como un valor central aún si no coincide con una de las modalidades.

La media es asociativa. Si reunimos dos muestras de tamaño

con medias $\overline{x}$ y $\overline{y}$ , respectivamente, entonces la media de la nueva muestra será $(n_x\overline{x} + n_y\overline{y})/(n_x+n_y)$ .

Si $(x_1,\ldots,x_n)$ es una muestra y si para todo $i=1,\ldots,n$ , escribimos

donde

son dos constantes, entonces la media empírica de la muestra $(y_1,\ldots,y_n)$ es $\overline{y} = a\overline{x} + b$ . En particular si

y $b=-\overline{x}$ , la nueva muestra tiene una media nula. Centrar los datos es sustraerles su media empírica para así llevarla a 0.

Un caso particular importante es el de los datos binarios. Frecuentemente debemos construir una muestra binaria a partir de una muestra numérica, para reagruparla en clases. Sea

un subconjunto de $\mathbb {R}$ (un intervalo en el caso de una clase). Denotemos por $\mathbb {I}_A(x)$ su función indicatriz que vale

si $x\in A$ , 0 si no. Si $(x_1,\ldots,x_n)$ es una muestra que toma valores reales, entonces $(\mathbb {I}_A(x_1),\ldots,\mathbb {I}_A(x_n))$ es una muestra binaria y su media empírica recibe el nombre de frecuencia empírica de

. Es simplemente la proporción de los valores de $(x_1,\ldots,x_n)$ que pertenecen a

Uno de los inconvenientes de la media empírica, vista como valor central de una muestra, es ser sensible a valores extremos. Un valor que es evidentemente muy diferente de los otros es calificado frecuentemente de valor aberrante. Que él sea el resultado de un error en la recolección o en la transcripción, no se le puede considerar como representativo. Supongamos que en una muestra de

valores todos sean del orden de

, excepto uno, que es de el orden de

. La media empírica será del orden de

, es decir muy lejana de la mayoría de los valores de la muestra. Para paliar este inconveniente, podemos decidir no tomar en cuenta los valores extremos para el cálculo de la media. Obtenemos entonces una media podada (en inglés ''trimmed mean'').

Definición 1.2 Sea $(x_1,\ldots,x_n)$ una muestra y $\alpha$ un número real entre 0 y

. La media podada de nivel $1\!-\!\alpha$ es la media empírica de la muestra sin considerar un número de valores extremos igual a la parte entera de $n\alpha$ . Diremos que se poda a la derecha, a la izquierda o bilateralmente según se supriman los valores más pequeños, los más grandes o a la vez los más pequeños y los más grandes respectivamente.

En estadística los números reales $\alpha$ entre 0 y

son una tradición. La misma tradición hace que se les asigne prioritariamente los valores

, menos frecuentemente

. Por tanto debemos ver a $\alpha$ como ''una proporción débil'', y a $1\!-\!\alpha$ como ''una proporción fuerte''.

Como una técnica de primera aproximación en el alisamiento de las series cronológicas, se emplean las medias móviles, que son las medias aritméticas de los valores que se encuentran alrededor de la fecha que se considera.

Definición 1.3 Sea $(x_1,\ldots,x_n)$ una serie cronológica y $k\geq 0$ un entero. Llamamos serie de las medias móviles de orden

, a la serie $(m_{k+1},\ldots,m_{n-k})$ definida para todo $h=k\!+\!1,\ldots,n\!-\!k$ , por:

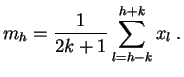
$\displaystyle m_h = \frac{1}{2k+1} \sum_{l=h-k}^{h+k} x_l\;.$

El inconveniente de las medias móviles es asociar a una fecha dada una media aritmética que no otorga más peso al valor original correspondiente a esa fecha que a los otros. A veces se emplea una ponderación exponencialmente decreciente con respecto al intervalo de tiempo a la fecha que se toma como centro. Se realiza así un alisamiento exponencial.

Definición 1.4 Sea $(x_1,\ldots,x_n)$ una serie cronológica,

un entero y $\rho$ un número real comprendido estrictamente entre 0 y

. El alisamiento exponencial de la serie, de orden

y de peso $\rho$ , es la serie $(r_{k+1},\ldots,r_{n-k})$ definida para todo $h=k\!+\!1,\ldots,n\!-\!k$ por:

$\displaystyle r_h = \frac{1-\rho }{1+\rho-2\rho^{k+1}} \sum_{l=-k}^{+k} \rho^{\vert l\vert} x_{h+l}\;.$