En un problema de
regresión, los carácteres no son considerados de la misma forma.
Uno de ellos es el carácter ''a explicar'', los
otros son ''explicativos''. Vamos
primero a considerar el caso de dos carácteres, ![]() (explicativo)
e
(explicativo)
e ![]() (a explicar). ''Explicar'' significa aquí expresar una
dependencia funcional de
(a explicar). ''Explicar'' significa aquí expresar una
dependencia funcional de ![]() como función de
como función de ![]() , de manera tal de
prever el valor de
, de manera tal de
prever el valor de ![]() conociendo el de
conociendo el de ![]() . Si para todo
individuo
. Si para todo
individuo ![]() ,
,
![]() , y si se observa un valor
, y si se observa un valor ![]() del carácter
del carácter ![]() en un nuevo individuo, daremos
en un nuevo individuo, daremos
![]() como
predicción del carácter
como
predicción del carácter ![]() en este nuevo individuo. La situación
ideal donde
en este nuevo individuo. La situación
ideal donde ![]() no se encuentra nunca en la práctica. Más
bien se buscará, en una familia fija de funciones, aquella para la
que los
no se encuentra nunca en la práctica. Más
bien se buscará, en una familia fija de funciones, aquella para la
que los ![]() se encuentran más cerca de los
se encuentran más cerca de los ![]() . La
cercanía se mide en general por el
error cuadrático
medio:
. La
cercanía se mide en general por el
error cuadrático
medio:
Hablamos entonces de regresión en el sentido de los mínimos
cuadrados. Las diferencias entre los
valores observados ![]() y los valores que predice el modelo
y los valores que predice el modelo
![]() , se llaman los
residuos.
Si el modelo se ajusta de manera tal que
la serie de los residuos sea centrada (de media nula), entonces el
error cuadrático
, se llaman los
residuos.
Si el modelo se ajusta de manera tal que
la serie de los residuos sea centrada (de media nula), entonces el
error cuadrático ![]() es la varianza de los residuos. La
regresión
lineal consiste en buscar
es la varianza de los residuos. La
regresión
lineal consiste en buscar ![]() entre las funciones
afines. La solución se expresa de manera simple a partir de las
carácterísticas de
entre las funciones
afines. La solución se expresa de manera simple a partir de las
carácterísticas de ![]() e
e ![]() .
.
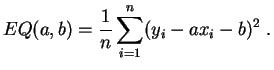
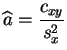 y
y
Demostración:
Si fijamos ![]() ,
, ![]() es un polinomio de grado
es un polinomio de grado ![]() en
en ![]() . El
alcanza su mínimo para un
. El
alcanza su mínimo para un ![]() tal que la derivada se anule.
Calculando:
tal que la derivada se anule.
Calculando:
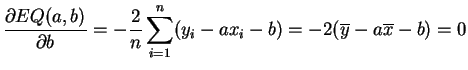
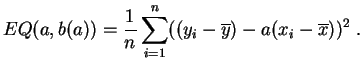
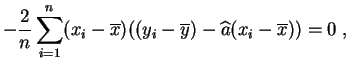
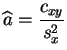 y
y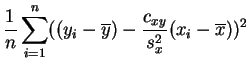 |
|||
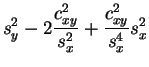 |
|||
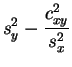 |
|||
Es importante observar la diferencia de los roles que
desempeñan ![]() e
e ![]() . Geométricamente, la
recta
de regresión lineal de
. Geométricamente, la
recta
de regresión lineal de ![]() con respecto a
con respecto a ![]() minimiza la suma de
las distancias verticales de los puntos
minimiza la suma de
las distancias verticales de los puntos ![]() a la recta. La recta
de regresión lineal de
a la recta. La recta
de regresión lineal de ![]() con respecto a
con respecto a ![]() minimiza las
distancias horizontales. Las dos rectas se cortan en el centro de
gravedad,
minimiza las
distancias horizontales. Las dos rectas se cortan en el centro de
gravedad,
![]() , de la nube de puntos. La
separación entre las dos rectas es mayor cuando la
correlación es
más débil.
, de la nube de puntos. La
separación entre las dos rectas es mayor cuando la
correlación es
más débil.
La predicción es la primera aplicación de la regresión
lineal. A continuación tenemos las estaturas en centímetros
(muestra ![]() ) y el peso en kilogramos (
) y el peso en kilogramos (![]() ) de
) de ![]() niños de
niños de ![]() años.
años.

Hacer una
regresión lineal quiere decir que se piensa que el peso
debe crecer, en general, proporcionalmente a la estatura. La recta
de regresión lineal constituye un modelo de predicción. Por
ejemplo diremos que el peso promedio de un niño de 6 años que mide
120 centímetros será de
![]() kg.
Evidentemente esta predicción no es infalible. Ella sólo da un
orden de magnitud. El valor observado será probablemente distinto
y el error previsible será del orden de
kg.
Evidentemente esta predicción no es infalible. Ella sólo da un
orden de magnitud. El valor observado será probablemente distinto
y el error previsible será del orden de
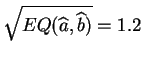 kg.
kg.
Como segunda aplicación se puede extender el
ajuste por
cuantiles a familias de leyes
invariantes por transformaciones afines, como las
leyes
normales .
Sea ![]() una muestra continua de tamaño
una muestra continua de tamaño ![]() para la cual queremos
verificar si ella podría haber salido de una ley normal
para la cual queremos
verificar si ella podría haber salido de una ley normal
![]() , con parámetros
, con parámetros ![]() y
y ![]() desconocidos. Para
desconocidos. Para
![]() , denotemos como siempre por
, denotemos como siempre por
![]() los
estadígrafos
de orden. Si la hipótesis de normalidad
es pertinente, entonces
los
estadígrafos
de orden. Si la hipótesis de normalidad
es pertinente, entonces ![]() debe estar cerca del cuantil
debe estar cerca del cuantil
![]() de la ley
de la ley
![]() . Recordemos que si una variable aleatoria
. Recordemos que si una variable aleatoria ![]() sigue la ley
sigue la ley
![]() , entonces
, entonces
![]() sigue la
ley
sigue la
ley
![]() . Esto es lo mismo que decir que para
todo
. Esto es lo mismo que decir que para
todo
![]() :
:
Denotemos por
![]() los valores de la
función cuantil de la ley
los valores de la
función cuantil de la ley
![]() en los puntos
en los puntos ![]() . Si
la hipótesis de normalidad se verifica, los puntos de coordenadas
. Si
la hipótesis de normalidad se verifica, los puntos de coordenadas
![]() deberían estar cercanos de la recta de ecuación
deberían estar cercanos de la recta de ecuación
![]() . Una
regresión
lineal de las
. Una
regresión
lineal de las ![]() con
respecto a las
con
respecto a las ![]() nos da a la vez una estimación de los valores
de
nos da a la vez una estimación de los valores
de ![]() y
y ![]() , y una indicación sobre la calidad del ajuste
(figura 15).
Antes de que existieran los programas de cálculo, se vendía papel
''gausso-aritmético'', graduado en las abscisas según los
cuantiles de la ley
, y una indicación sobre la calidad del ajuste
(figura 15).
Antes de que existieran los programas de cálculo, se vendía papel
''gausso-aritmético'', graduado en las abscisas según los
cuantiles de la ley
![]() . Bastaba poner en las
ordenadas los valores de las
. Bastaba poner en las
ordenadas los valores de las ![]() para trazar a mano la recta
de regresión lineal, que lleva el nombre de
''recta de Henry'', por el nombre del
coronel que inventó este método en el siglo XIX para estudiar el
alcance de los cañones.
para trazar a mano la recta
de regresión lineal, que lleva el nombre de
''recta de Henry'', por el nombre del
coronel que inventó este método en el siglo XIX para estudiar el
alcance de los cañones.
El problema de la regresión es determinar en una familia de funciones dada, cual es la función que minimiza el error cuadrático (3.2). Pero es frecuente que no haya una solución explícita. Para ciertas familias de funciones, se transforma el problema de manera tal de llevarlo a una regresión lineal. Presentamos aquí algunos casos frecuentes.
Como ejemplo de aplicación, vamos a tomar el problema del ajuste
por los
cuantiles para la
familia de
leyes de Weibull, las cuales
se emplean frecuentemente para modelar tiempos de sobrevida en
medicina o tiempos de funcionamiento en fiabilidad. La función
cuantil de la ley de Weibull
![]() es:
es:
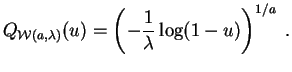
Sea ![]() una muestra que queremos ajustar por una ley de Weibull de
parámetros
una muestra que queremos ajustar por una ley de Weibull de
parámetros ![]() y
y ![]() desconocidos. Para
desconocidos. Para
![]() , el
estadígrafo de orden
, el
estadígrafo de orden ![]() debe estar cerca del cuantil
debe estar cerca del cuantil
![]() .
.
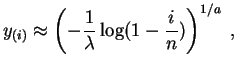
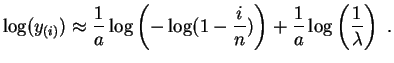
Pongamos
![]() y
y
![]() . Los
puntos
. Los
puntos
![]() deberían estar cerca de la recta de ecuación
deberían estar cerca de la recta de ecuación
![]() . Una regresión lineal nos dará no
solamente los valores para
. Una regresión lineal nos dará no
solamente los valores para ![]() y
y ![]() , sino también una
indicación sobre la calidad del ajuste. Antes de los programas de
cálculo, existía también un ''papel Weibull'', graduado de manera
tal que se podía automatizar este caso particular de regresión
no lineal.
, sino también una
indicación sobre la calidad del ajuste. Antes de los programas de
cálculo, existía también un ''papel Weibull'', graduado de manera
tal que se podía automatizar este caso particular de regresión
no lineal.