Sección : Datos bidimensionales
Previo : Representaciones bidimensionales
Siguiente : Regresión lineal simple

Covarianza

Si dos carácteres cuantitativos $x$ e $y$ son medidos en $n$ individuos, podemos considerar a la muestra bidimensional como una nube de $n$ puntos en $\mathbb {R}^2$. Diferentes carácterísticas estadísticas permiten resumir la información contenida en su forma. Si $\overline{x}$ e $\overline{y}$ denotan a las medias empíricas de los dos carácteres, el punto $(\overline{x},\overline{y})$ es el centro de gravedad de la nube. Las varianzas empíricas $s_x^2$ y $s_y^2$ evidencian la dispersión de abscisas y de ordenadas. Para ir más allá en la descripción, hay que calcular la covarianza.

Definición 3.1   Llamamos covarianza de $x$ e $y$, y denotamos por $c_{xy}$, a la cantidad:

$$c_{xy} = \frac{1}{n} \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})\;.$$

Esta definición extiende la de la varianza en la medida en que $s^2_x = c_{xx}$. La covarianza es simétrica ( $c_{xy}=c_{yx}$) y bilineal: si $x$ y $x'$ son dos muestras de tamaño $n$, $a$ y $a'$ dos números reales y denotamos $x^*=ax+a'x'$, entonces:

$$c_{x^*y} = ac_{xy} + a' c_{x'y}\;.$$

Como consecuencia de la bilinealidad tenemos:

$$s^2_{x+y} = s_x^2 + s_y^2 + 2c_{xy}\;.$$

En la práctica, para el cálculo, se emplea la siguiente fórmula:

Proposición 3.2   La covarianza de $x$ e $y$ se escribe:

$$c_{xy} = \frac{1}{n} \sum_{i=1}^n x_iy_i\;-\overline{x}\,\overline{y}\;.$$

La covarianza es la media de los productos menos el producto de las medias.

Demostración:  Basta desarrollar los productos:

$$c_{xy} = \frac{1}{n} \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})$$

$$= \frac{1}{n} \sum_{i=1}^n (x_iy_i-\overline{x}y_i -x_i\overline{y} +\overline{x}\,\overline{y})$$

$$= \Big(\frac{1}{n} \sum_{i=1}^n x_iy_i\Big)-\overline{x}\,\overline{y}\;.$$

$\square$

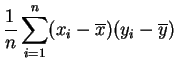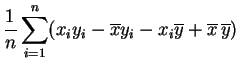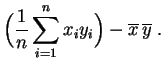La covarianza se compara al producto de las desviaciones estándar empleando la desigualdad de Cauchy-Schwarz.

Proposición 3.3   Tenemos:

$$\vert c_{xy}\vert \leq s_x\,s_y\;.$$ (3.1)

Demostración:  Sea $a$ un número real arbitrario. Calculemos la varianza de $ax+y$:

$$s^2_{ax+y} = a^2s_x^2 + 2ac_{xy} + s_y^2\;.$$

Este valor es positivo o nulo para todo $a$. Por tanto el discriminante de la expresión de $s^2_{ax+y}$, visto como un trinomio en $a$, es necesariamente negativo. Su valor es:

$$c_{xy}^2 - s_x^2s_y^2\;,$$

de aquí se obtiene la desigualdad buscada. Observemos que el discriminante es nulo si y sólo si $s^2_{ax+y}$ se anula, es decir si existe un $a$ tal que $ax+y$ es constante. Por tanto la expresión 3.1 no es una igualdad a menos que exista una relación afín entre $x$ e $y$. $\square$

A partir de la desigualdad 3.1, parece natural dividir la covarianza por el producto de las desviaciones estándar, para así definir el coeficiente de correlación (las desviaciones estándar se suponen no nulas).

Definición 3.4   Llamamos coeficiente de correlación de $x$ e $y$, y denotamos $r_{xy}$, a la cantidad:

$$r_{xy} = \frac{c_{xy}}{ s_x\,s_y}\;.$$

Cualesquiera que sean las unidades y los ordenes de magnitud de $x$ e $y$, el coeficiente de correlación es un número sin unidades, comprendido entre $-1$ y $1$. Expresa la mayor o menor dependencia lineal entre $x$ e $y$ o, geométricamente, el mayor o menor aplastamiento de la nube de puntos. Hemos visto que la desigualdad 3.1 no podía ser una igualdad salvo si $x$ es constante o si $y$ es de la forma $ax+b$. Si $a$ es positivo, el coeficiente de correlación de $x$ con $ax+b$ es igual a $+\!1$, es igual a $-\!1$ si $a$ es negativo. Un coeficiente de correlación nulo o cercano a 0 significa que no hay relación lineal entre los carácteres, pero no conlleva ninguna noción de independencia más general. Consideremos, por ejemplo, las dos muestras:

$$\begin{array}{cccrrrrrrrl} x&=&(&-\!3&-\!2&-\!1&0&1&2&3&)\\ y&=&(&3&2&1&0&1&2&3&)\;. \end{array}$$

Su coeficiente de correlación es nulo y sin embargo $x$ e $y$ están ligados por una relación funcional ($y_i=\vert x_i\vert$).

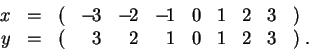
Cuando el coeficiente de correlación está cerca de $1$ o $-\!1$, los carácteres se dicen que están ''fuertemente correlados''. Hay que tener cuidado con la confusión frecuente entre correlación y causalidad. Que dos fenómenos estén correlados no implica, de ninguna manera, que uno sea causa del otro. Es muy frecuente que una correlación fuerte indica que los dos carácteres dependen de un tercero que no ha sido medido. Este tercer carácter se llama ''factor de confusión''. Que exista una fuerte correlación entre la recaudación de impuestos en Inglaterra y la criminalidad en el Japón, indica que ambos están ligados al aumento global de la población. El precio del trigo y la población de roedores están negativamente correlados, porque ambos dependen del nivel de la cosecha de trigo. Puede ser que una fuerte correlación exprese una verdadera causalidad, como entre el número de cigarrillos que se fuma al día y la aparición de un cáncer de pulmón. Pero no es la estadística la que demuestra la causalidad, ella permite solamente detectarla. La influencia del consumo del tabaco en la aparición de un cáncer de pulmón ha sido científicamente demostrada en la medida en que se pudieron analizar los mecanismos fisiológicos y bioquímicos que hacen que el alquitrán y la nicotina induzcan errores en la reproducción del código genético de las células.

Sección : Datos bidimensionales
Previo : Representaciones bidimensionales
Siguiente : Regresión lineal simple