On a vu à l'exercice 32 qu'étant donné deux triplets
![]() et
et
![]() de droites distinctes et concourantes d'un même plan affine, il existait toujours une transformation affine de ce plan transformant
de droites distinctes et concourantes d'un même plan affine, il existait toujours une transformation affine de ce plan transformant ![]() en
en ![]() ,
, ![]() en
en ![]() et
et ![]() en
en ![]() . Du point de vue de la géométrie affine, tous les triplets de droites distinctes et concourantes sont donc équivalents (de même que tous les triangles non aplatis le sont, puisque, étant donné deux triangles non aplatis
. Du point de vue de la géométrie affine, tous les triplets de droites distinctes et concourantes sont donc équivalents (de même que tous les triangles non aplatis le sont, puisque, étant donné deux triangles non aplatis ![]() et
et ![]() , il existe toujours une transformation affine du plan et une seule transformant
, il existe toujours une transformation affine du plan et une seule transformant ![]() en
en ![]() ,
, ![]() en
en ![]() et
et ![]() en
en ![]() ).
).
Il n'en va plus de même si on considère des quadruplets de droites concourantes. On peut en effet associer à tout tel quadruplet un nombre, appelé birapport ou rapport anharmonique des quatre droites, qui est invariant par toute transformation affine.
On commence par définir le birapport ![]() de quatre points distincts alignés
de quatre points distincts alignés ![]() ,
, ![]() ,
, ![]() ,
, ![]() comme le réel
comme le réel
![$\displaystyle [A,B,C,D]=\dfrac{\overline {AC} \; \overline {BD}}{\overline {AD} \; \overline {BC}}\; .$](img1049.gif)
Soit maintenant, dans un plan affine ![]() , quatre droites distinctes concourantes en un même point
, quatre droites distinctes concourantes en un même point ![]() et coupant deux droites
et coupant deux droites ![]() et
et ![]() en des points
en des points ![]() ,
, ![]() ,
, ![]() ,
, ![]() et
et ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Orientons
. Orientons ![]() et munissons-le d'un produit scalaire. Soit alors
et munissons-le d'un produit scalaire. Soit alors ![]() le projeté orthogonal de
le projeté orthogonal de ![]() sur
sur ![]() et
et ![]() un vecteur directeur unitaire de
un vecteur directeur unitaire de ![]() tel que le système
tel que le système
![]() soit direct. On a alors, en prenant les déterminants dans une base orthonormée directe :
soit direct. On a alors, en prenant les déterminants dans une base orthonormée directe :
![\includegraphics[width=0.6\textwidth]{figures/birapport}](img1060.gif)
Il en résulte que
![$\displaystyle [A,B,C,D]=\dfrac{\sin(\overrightarrow{OA},\overrightarrow{OC}) \;...
...{OA},\overrightarrow{OD}) \; \sin(\overrightarrow{OB},\overrightarrow{OC})}\; .$](img1061.gif)
Mais
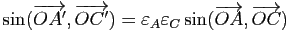 , où
, où
![]() (resp.
(resp.
![]() ) vaut
) vaut ![]() si les points
si les points ![]() et
et ![]() (resp.
(resp. ![]() et
et ![]() ) sont du même côté de
) sont du même côté de ![]() ,
, ![]() sinon. En écrivant des formules analogues pour les autres termes, on en déduit que
sinon. En écrivant des formules analogues pour les autres termes, on en déduit que
![]() . Ce nombre ne dépend donc pas de la sécante
. Ce nombre ne dépend donc pas de la sécante ![]() . On l'appelle birapport des quatre droites
. On l'appelle birapport des quatre droites ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Comme toute transformation affine conserve les rapports de mesures algébriques pour des points alignés, elle conserve a fortiori le birapport.
. Comme toute transformation affine conserve les rapports de mesures algébriques pour des points alignés, elle conserve a fortiori le birapport.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales