Sección : Tests no paramétricos
Previo : Tests no paramétricos
Siguiente : Test de Kolmogorov-Smirnov

Test sobre el valor de un cuantil

Aquí, como en todo el capítulo, el modelo básico es el de una muestra de una ley desconocida $P$. Por lo tanto suponemos que los datos son realizaciones de variables aleatorias independientes de una misma ley $P$. No se supone que esta ley pertenece a una familia paramétrica particular (de aquí el nombre de test no paramétrico). En un primer momento, la hipótesis ${\cal H}_0$ se referirá al valor de un cuantil de $P$.

Tomemos el caso de un tratamiento que se supone hace bajar los niveles de colesterol. Para cada individuo $i$ de un grupo de pacientes, se mide la diferencia $X_i$ entre los niveles de colesterol después y antes del tratamiento. Algunas de estas diferencias son negativas (disminución del nivel de colesterol) otras positivas (aumento). La hipótesis ${\cal H}_0$ es que el tratamiento no tiene un efecto significativo. Rechazaremos ${\cal H}_0$ (decidiremos que el tratamiento es eficaz) si se observa una cantidad suficiente de disminuciones. El estadígrafo de test es el número de descensos:

$$T= \sum_{i=1}^n \mathbb {I}_{(-\infty,0]}(X_i)\;,$$

La notación $\mathbb {I}_A(x)$ designa a la función indicatriz del conjunto $A$, que vale $1$ si $x\in A$ y 0 si no. Si ${\cal H}_0$ es verdadera, la mediana de la ley $P$ de las $X_i$ es nula y $T$ sigue la ley binomial ${\cal B}(n,0.5)$.

Generalizamos esta situación para el valor de un cuantil cualquiera.

Proposición 2.1   Sea $(X_1,\ldots,X_n)$ una muestra de la ley $P$, de función cuantil $Q$. Sea $u\in ]0,1[$ un número real fijo. Consideremos la hipótesis nula:

$${\cal H}_0\;:\; Q(u)=q_0\;,$$

donde $q_0$ es un número real fijo. Sea $T$ el número de elementos de la muestra, inferiores a $q_0$:

$$T= \sum_{i=1}^n \mathbb {I}_{(-\infty,q_0]}(X_i)\;.$$

Entonces bajo la hipótesis ${\cal H}_0$, $T$ sigue la ley binomial ${\cal B}(n,u)$.

El caso particular en el que $u=0.5$ y $q_0=0$, presentado en el ejemplo, lleva el nombre especial de test de signos. Supongamos que en un grupo de $46$ individuos se observaron $29$ descensos en el nivel de colesterol. El p-valor correspondiente es :

$$p(29) = 1-F_{{\cal B}(46,0.5)}(28) = 0.0519\;.$$

Para una muestra grande, se puede remplazar la ley binomial por su aproximación normal. Bajo ${\cal H}_0$, el estadígrafo:

$$T' = \frac{T-nu}{\sqrt{nu(1\!-\!u)}}\;,$$

que está centrado y reducido, sigue la ley normal ${\cal N}(0,1)$. En el ejemplo que hemos visto, $T'$ toma el valor $1.7693$. El p-valor correspondiente es:

$$1-F_{{\cal N}(0,1)}(1.7693) = 0.0384\;.$$

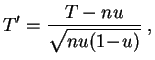
Es aconsejable limitar el uso de la aproximación por la normal únicamente a los casos en los que la ley no se pueda calcular exactamente.

Sección : Tests no paramétricos
Previo : Tests no paramétricos
Siguiente : Test de Kolmogorov-Smirnov