Sección : Estadígrafos de test
Previo : Reglas de decisión
Siguiente : Tests no paramétricos

Umbral y p-valor

La definición 1.4 del parrafo anterior hace aparecer el umbral como la probabilidad $\alpha$, fijada a priori, que el test rechace la hipótesis ${\cal H}_0$ erróneamente:

$$\mathbb {P}_{{\cal H}_0}[$$ Rechazo de $${\cal H}_0] = \alpha\;.$$

Una vez recogidos los datos, se calcula el valor que toma el estadígrafo del test, y la respuesta será binaria: rechazar o no ${\cal H}_0$. Muchas veces se prefiere retener la información contenida en el valor del estadígrafo del test, y dar el valor del umbral límite en el cual ${\cal H}_0$ hubiese sido rechazada, teniendo en cuenta lo observado. Tomemos el ejemplo (bastante frecuente) de una hipótesis ${\cal H}_0$ bajo la cual el estadígrafo del test sigue la ley normal ${\cal N}(0,1)$. La regla de rechazo para el test bilateral de umbral $0.05$ es:

   Rechazo de $${\cal H}_0\;\Longleftrightarrow\; T\notin[-1.96\,,\,+1.96]\;.$$

Supongamos que el valor que toma $T$ sea $2.72$. La hipótesis ${\cal H}_0$ será rechazada. Pero ella también sería rechazada al nivel $0.01$. De hecho ella sería rechazada a cualquier nivel de umbral superior a $0.00653$, lo que es una información mucho más precisa que una simple respuesta binaria.

Definición 1.7   Sea ${\cal H}_0$ la hipótesis nula, $T$ el estadígrafo de test y $F_0$ su función de distribución bajo la hipótesis ${\cal H}_0$. Se supone que $F_0$ es continua.

1. Para un test bilateral (rechazo de los valores muy alejados) el p-valor de un valor $t$ tomado por $T$ es:

   $$p(t) = \left\{ \begin{array}{lcl} 2F_0(t) &\mbox{si}&F_0... ..._0(t)) &\mbox{si}&F_0(t)\geq 0.5\;.\\ \end{array} \right.$$

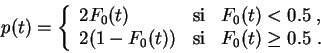
2. Para un test unilateral a la derecha (rechazo de los valores muy grandes) el p-valor de un valor $t$ tomado por $T$ es:

   $$p(t) = 1-F_0(t)\;.$$

3. Para un test unilateral a la izquierda (rechazo de los valores muy pequeños) el p-valor de un valor $t$ tomado por $T$ es:

   $$p(t) = F_0(t)\;.$$

Sin embargo, calcular un p-valor para un test bilateral es bastante artificial. De acuerdo con el valor que tome $T$ , se tratará más bien de realizar un test unilateral encaminado a decidir si el valor observado es demasiado grande o demasiado pequeño. Para un estadígrafo de test que sigue la ley ${\cal N}(0,1)$, el valor $2.72$ se encuentra claramente a la derecha de la distribución : el problema que se plantea no es de saber si es muy pequeño, si no más bien si es significativamente grande. En la práctica, para un estadígrafo de test con una función de distribución $F_0$ bajo ${\cal H}_0$, se definirá frecuentemente el p-valor del valor $t$ por:

$$p(t) = \min \{F_0(t)\,,\,1\!-\!F_0(t)\}\;.$$

 

El conocer el p-valor, hace inútil el cálculo previo de la región de rechazo: si $p(t)$ es el p-valor de una observación de $T$ bajo la hipótesis ${\cal H}_0$, obtenemos un test de umbral $\alpha$ con la siguiente regla de rechazo:

   Rechazo de $${\cal H}_0\;\Longleftrightarrow\; p(T)<\alpha\;.$$

En el caso continuo, esto se convierte en reemplazar el estadígrafo $T$ por $F_0(T)$ o $1-F_0(T)$. Bajo la hipótesis ${\cal H}_0$, estos dos estadígrafos siguen la ley uniforme ${\cal U}(0,1)$.
 

Cuando el estadígrafo de test es discreto, hace falta incluir el valor observado en el intervalo de que se le calcula la probabilidad. Para un test unilateral a la izquierda, esto no introduce ningún cambio: $F_0(t)$ es la probabilidad de que $T$ sea inferior o igual a $t$. Para un test unilateral a la derecha sobre una variable que toma valores en $\mathbb {N}$ (el caso más frecuente) habrá que calcular $1-F_0(t\!-\!1)$. Supongamos, por ejemplo, que la ley de $T$ sea la ley binomial ${\cal B}(100,0.5)$, el p-valor de $60$ es la probabilidad de que $T$ sea superior o igual a $60$ es decir:

$$1-F_{{\cal B}(100,0.5)}(59) = 0.0284\;.$$

Sección : Estadígrafos de test
Previo : Reglas de decisión
Siguiente : Tests no paramétricos