Sección : Estadígrafos de test
Previo : Modelos probabilistas rechazables
Siguiente : Umbral y p-valor

Reglas de decisión

Se ha seleccionado un modelo probabilista, que hace que los datos observados sean realizaciones de variables aleatorias. Denotemos por $(x_1,\ldots,x_n)$ los datos y por $(X_1,\ldots,X_n)$ las variables aleatorias que los modelan. Sobre la ley de estas variables aleatorias se plantean un cierto número de hipótesis que no se pondrán en duda. Una hipótesis en particular, ${\cal H}_0$, será sometida a test. La decisión dependerá del valor que tome una cierta función de los datos que llamaremos $\tau$:

$$T=\tau(X_1,\ldots,X_n)\;.$$

En el modelo, $T$ es una variable aleatoria, el estadígrafo del test. Se selecciona de manera tal que su ley de probabilidad bajo la hipótesis ${\cal H}_0$ es conocida. Denotamos esta ley por $P_0$. Si los $x_i$ son realizaciones de las $X_i$, entonces $t=\tau(x_1,\ldots,x_n)$ es el valor que toma $T$. El test consiste en rechazar la hipótesis ${\cal H}_0$ cuando el valor de $t$ es muy poco verosímil para $P_0$.

Para la ley de probabilidad $P_0$, los valores más plausibles están contenidos dentro de sus intervalos de dispersión. Estos se expresan con la ayuda de la función cuantil. Si $T$ es una variable aleatoria, la función cuantil de la ley de $T$ es la función que va de $[0\,,1]$ en $\mathbb {R}$, y que a cada $u\in [0\,,1]$ asocia el valor:

$$Q_T(u) = \inf\{t$$ t.q. $$\mathbb {P}[T\leq t]\geq u\}\;.$$

Es la inversa de la función de distribución. Las funciones cuantiles más usadas, tal y como lo están las funciones de distribución de las leyes usuales, están programadas en la mayoría de los sistemas de cálculo.

Definición 1.3   Sea $T$ une variable aleatoria y $\alpha$ un número real entre 0 y $1$. Llamamos intervalo de dispersión de nivel $1\!-\!\alpha$ a todo intervalo de la forma:

$$[\,Q_T(\alpha')\,,\,Q_T(1-\alpha+\alpha')\,]\;,$$   con$$\; 0\leq \alpha'\leq \alpha\;.$$

En estadística emplear números reales $\alpha$ entre 0 y $1$ constituye una tradición. La misma tradición hace que se les asigne prioritariamente los valores $0.05$ y $0.01$, menos frecuentemente $0.02$, $0.005$ ó $0.001$. Por tanto debemos leer $\alpha$ como ''una proporción débil'', y $1\!-\!\alpha$ como ''una proporción fuerte''. Un intervalo de dispersión de nivel $1\!-\!\alpha$ para $T$ es uno tal que $T$ pertenece a ese intervalo con probabilidad $1\!-\!\alpha$. El contiene, por tanto, a una fuerte proporción de los valores que tomará $T$ aún cuando el sea mucho más pequeño que el soporte de la ley. Según los valores de $\alpha'$, decimos que un intervalo de dispersión de nivel $1\!-\!\alpha$ es:

$\bullet$

unilateral inferior si $\alpha'=0$,

$\bullet$

unilateral superior si $\alpha'=\alpha$,

$\bullet$

simétrico si $\alpha'=\alpha/2$,

$\bullet$

optimal si su amplitud es la más pequeña de entre todos los intervalos de dispersión de nivel $1\!-\!\alpha$.

Presentamos los intervalos de dispersión unilaterales y simétricos, de nivel $0.95$ y $0.99$ para la ley normal ${\cal N}(0,1)$.

$$\begin{array}{\vert c\vert c\vert c\vert c\vert} \hline \... ....5758\\ 0.01&0.01&-2.3263&+\infty\\ \hline \end{array}$$

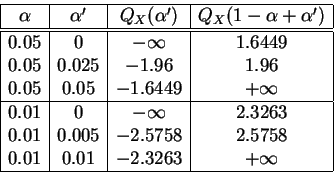
Cuando la ley de la variable aleatoria $T$ es discreta, la noción de intervalo de dispersión puede contener alguna ambigüedad. Consideremos, por ejemplo, la ley binomial ${\cal B}(10,0.6)$. Veamos los valores de su función de distribución.

$i$	0	1	2	3	4	5	6	7	8	9	10
$F(i)$	0.000	0.002	0.012	0.055	0.166	0.367	0.618	0.833	0.954	0.994	1

Fijemos $1\!-\!\alpha=0.9$. En todo rigor, el valor de la función cuantil en el punto $0.9$ es $7$. El intervalo $[0,7]$ debería ser por tanto un intervalo de dispersión de nivel $0.9$ para la ley ${\cal B}(10,0.6)$. Sin embargo su probabilidad es de $0.833$. Para los cálculos que emplean intervalos de dispersión, siempre se aplica un principio de precaución, el cual consiste en garantizar el nivel. Por tanto consideraremos como intervalos de dispersión de nivel $1\!-\!\alpha$ sólo a aquellos cuya probabilidad es mayor o igual a $1\!-\!\alpha$. Este principio lleva a modificar la definición 1.3 para las leyes discretas que toman valores en $\mathbb {N}$, reemplazando el borde derecho $Q_T(1-\alpha+\alpha')$, por $1+Q_T(1-\alpha+\alpha')$. La tabla que mostramos a continuación nos da una lista de intervalos de dispersión de nivel $\geq 0.9$, conjuntamente con su probabilidad exacta, para la ley ${\cal B}(10,0.6)$.

Intervalo	$[0,8]$	$[1,8]$	$[2,8]$	$[3,8]$	$[4,9]$	$[4,10]$
Probabilidad	0.954	0.954	0.952	0.941	0.939	0.945

Dos de los intervalos tienen amplitud mínima, $[3,8]$ y $[4,9]$. Seleccionaremos a aquél que tiene la mayor probabilidad, es decir a $[3,8]$. La figura 2 representa en función de $p$ los intervalos de dispersión optimales, en el sentido que hemos definido anteriormente, para la ley binomial ${\cal B}(10,p)$, así como los intervalos de dispersión simétricos.

 

Hacer un test consiste en rechazar la hipótesis ${\cal H}_0$ si el valor que toma el estadígrafo del test cae fuera del intervalo de dispersión del nivel dado.

Proposición 1.4   Sea ${\cal H}_0$ una hipótesis y $\alpha$ un número real entre 0 y $1$. Se define un test de umbral $\alpha$ o test de nivel $\alpha$ para ${\cal H}_0$ por la regla de decisión:

   Rechazo de $${\cal H}_0\;\Longleftrightarrow\; T\notin I_\alpha\;,$$

donde:

$\bullet$

$T$ es un estadígrafo de test,

$\bullet$

$I_\alpha$ es un intervalo de dispersión de nivel $1\!-\!\alpha$ para la ley de $T$ bajo la hipótesis ${\cal H}_0$.

Al complemento de $I_\alpha$ se le llama región de rechazo. Si ${\cal H}_0$ es verdad, el umbral $\alpha$ es la probabilidad de que el valor que toma $T$ se encuentre fuera de $I_\alpha$, y por tanto que ${\cal H}_0$ sea rechazada erróneamente:

$$\mathbb {P}_{{\cal H}_0}[\,$$Rechazo de $${\cal H}_0\,] = \alpha\;.$$

Hasta ahora hemos dejado una gran flexibilidad para seleccionar el intervalo de dispersión. Los intervalos más usados son simétricos o unilaterales.

Definición 1.5   Se dice que un test es:

$\bullet$

unilateral si la región de rechazo es el complemento de un intervalo de dispersión unilateral.

$\bullet$

bilateral si la región de rechazo es el complemento de un intervalo de dispersión simétrico.

En el caso de la eficiencia de un medicamento, con el número de enfermos curados como estadígrafo del test, seleccionaremos un test unilateral (el tratamiento es ineficaz si la frecuencia de curados es muy débil, y es eficaz si la frecuencia es lo suficientemente grande). Para probar un generador pseudo-aleatorio, con el número de resultados entre $0.4$ y $0.9$ como estadígrafo del test, rechazaremos tanto los valores muy grandes como los muy pequeños y el test será bilateral.

En la definición que damos a continuación resumimos los tres tipos de test usuales.

Definición 1.6   Sean ${\cal H}_0$ la hipótesis nula, $\alpha$ el umbral, $T$ el estadígrafo del test y $Q_0$ su función cuantil bajo la hipótesis ${\cal H}_0$.

1. El test bilateral (rechazo de los valores muy alejados) está definido por la regla de decisión:
      Rechazo de $${\cal H}_0\,\Longleftrightarrow\; T\notin [Q_0(\alpha/2)\,,\,Q_0(1\!-\!\alpha/2)]\;.$$

2. El test unilateral a la derecha (rechazo de los valores muy grandes) está definido por la regla de decisión:
      Rechazo de $${\cal H}_0\,\Longleftrightarrow\; T > Q_0(1\!-\!\alpha)\;.$$

3. El test unilateral a la izquierda (rechazo de los valores muy pequeños) está definido por la regla de decisión:
      Rechazo de $${\cal H}_0\,\Longleftrightarrow\; T < Q_0(\alpha)\;.$$

Supongamos que el estadígrafo de test $T$ sigue, bajo la hipótesis ${\cal H}_0$, la ley binomial ${\cal B}(100,0.5)$, igual que en el ejemplo del generador pseudo-aleatorio. El intervalo de dispersión simétrico de nivel $\alpha=0.05$ es $[40\,,\,60]$. El test bilateral de umbral $0.05$ consistirá en rechazar ${\cal H}_0$ si el estadígrafo de test toma valores inferiores a $40$ o superiores a $60$. Para la ley binomial, como para otras leyes, podemos decidir de utilizar la aproximación por la ley normal: si $n$ es lo suficientemente grande, la ley ${\cal B}(n,p)$ está cerca de la ley normal que tiene la misma esperanza y la misma varianza que ella. En este caso la ley de $T$ está cerca de la ley ${\cal N}(50,25)$. El intervalo de dispersión simétrico de nivel $0.95$ para esta ley es $[40.2\,,\,59.8]$. Según este intervalo, deberíamos rechazar también los valores $40$ y $60$. Este tipo de aproximación era muy corriente hacerla cuando solamente se disponía de tablas de cuantiles. Ya en la actualidad los sistemas de cálculo que existen son capaces de calcular en forma precisa cualquier cuantil de las leyes usuales. Como regla general debe evitarse emplear un resultado de aproximación cuando se puede calcular exactamente. Los cuantiles de la ley ${\cal N}(50,25)$ nunca estuvieron en las tablas. Para calcularlos, se empleaban los de la ley ${\cal N}(0,1)$, reemplazando al estadígrafo de test $T$ por su valor centrado y reducido:

$$T'=\frac{T-50}{\sqrt{25}}\;.$$

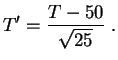
Si admitimos que la variable $T'$ sigue la ley ${\cal N}(0,1)$, el test bilateral de umbral $0.05$ consiste en rechazar todo valor que se encuentre fuera del intervalo de dispersión $[-\!1.96\,,\,+\!1.96]$. Esto es, evidentemente, equivalente a rechazar los valores de $T$ que se encuentren fuera del intervalo $[40.2\,,\,59.8]$. Hay otras transformaciones posibles. Si $T'$ sigue la ley ${\cal N}(0,1)$, entonces $T''=(T')^2$ sigue la ley chi-cuadrado ${\cal X}^2(1)$. Rechazar los valores de $T'$ que se encuentran fuera del intervalo $[-\!1.96\,,\,+\!1.96]$ es equivalente a rechazar los valores de $T''$ mayores que $(1.96)^2=3.841$, que es efectivamente el cuantil de orden $0.95$ de la ley ${\cal X}^2(1)$. Notemos que un test bilateral sobre el estadígrafo $T'$ es equivalente a un test unilateral a la derecha sobre el estadígrafo $T''$.
 
Los capítulos 2 y 3 contienen los ejemplos más clásicos de tests, primero con los cuantiles y después en el marco gaussiano. No siempre precisaremos si se trata de tests bilaterales o unilaterales. Lo importante es describir la hipótesis ${\cal H}_0$, el estadígrafo de test $T$ y su ley bajo ${\cal H}_0$. Decidir si el test debe ser unilateral a la izquierda, unilateral a la derecha o bilateral es muy frecuentemente un problema de sentido común.

Sección : Estadígrafos de test
Previo : Modelos probabilistas rechazables
Siguiente : Umbral y p-valor