Retomamos el problema de contrastar o hacer un test
entre dos hipótesis simples cuando el modelo es el de una
muestra
![]() de una ley de probabilidad desconocida
de una ley de probabilidad desconocida
![]() :
:
Los tests que tienen que ver con dos valores fijos de un parámetro son un caso particular de estos. Consideremos por ejemplo la serie de 10 datos binarios siguiente:
El modelo es una muestra de tamaño ![]() de la
ley
de Bernoulli de
parámetro
de la
ley
de Bernoulli de
parámetro ![]() , para la cual queremos hacer un test:
, para la cual queremos hacer un test:
La idea consiste en comparar las probabilidades de la
observación bajo cada una de las dos hipótesis. Para la ley de
Bernoulli de parámetro ![]() , la probabilidad que una
observación contenga
, la probabilidad que una
observación contenga ![]() ``
``![]() '' y
'' y ![]() ``0'' es
``0'' es
![]() o
sea
o
sea
![]() para
para ![]() y
y
![]() para
para ![]() .
Las dos son débiles, pero el cociente está a favor de
.
Las dos son débiles, pero el cociente está a favor de
![]() .
.
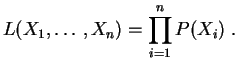
La interpretación es la siguiente. Por
definición, las variables aleatorias
![]() son
independientes y de misma ley
son
independientes y de misma ley ![]() . Por tanto la probabilidad que
la muestra teórica
. Por tanto la probabilidad que
la muestra teórica
![]() tenga por realización la
muestra observada
tenga por realización la
muestra observada
![]() es el producto de las
probabilidades para que
es el producto de las
probabilidades para que ![]() tome el valor
tome el valor ![]() , es decir:
, es decir:
En el caso de un modelo continuo, la ley ![]() tiene una densidad
con valores en
tiene una densidad
con valores en
![]() , y la probabilidad de que la muestra tome un
valor particular es siempre nula. Por tanto hay que sustituir la
probabilidad
, y la probabilidad de que la muestra tome un
valor particular es siempre nula. Por tanto hay que sustituir la
probabilidad ![]() por su densidad en la definición de la
verosimilitud.
por su densidad en la definición de la
verosimilitud.
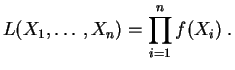
La interpretación es la siguiente. Sea
![]() un número
real estrictamente positivo (pequeño). La probabilidad que la
muestra
un número
real estrictamente positivo (pequeño). La probabilidad que la
muestra
![]() tenga una realización ``tan cerca
como
tenga una realización ``tan cerca
como
![]() '' de la muestra observada
'' de la muestra observada
![]() puede escribirse:
puede escribirse:
![$\displaystyle \mathbb {P}\Big[X_1\in
[x_1\!-\!\frac{\varepsilon}{2},x_1\!+\!\frac{\varepsilon}{2}]$](img491.gif) y y ![$\displaystyle X_n\in
[x_n-\frac{\varepsilon}{2},x_n+\frac{\varepsilon}{2}]\Big]$](img493.gif) |
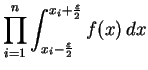 |
||
 |
|||
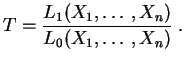
Se llama test del
cociente de verosimilitud de umbral
![]() , al test definido por la regla de decisión:
, al test definido por la regla de decisión:
En el caso en que la ley ![]() es discreta, la ley del estadígrafo
de test
es discreta, la ley del estadígrafo
de test ![]() lo es también, y la definición de la región de
rechazo para un valor fijado del
umbral
lo es también, y la definición de la región de
rechazo para un valor fijado del
umbral ![]() plantea los
problemas habituales. En la práctica, es mejor calcular el
p-valor.
plantea los
problemas habituales. En la práctica, es mejor calcular el
p-valor.
Retomemos el ejemplo de una muestra de la ley de Bernoulli, con las dos hipótesis:
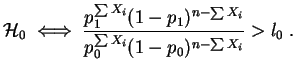
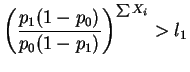 |
|||
Por tanto no se rechazará
![]() .
.
Veamos otro ejemplo, con dos leyes continuas.
Las leyes
![]() y
y
![]() tienen por densidades
respectivas :
tienen por densidades
respectivas :
La regla de decisión del test del cociente de verosimilitud
será:
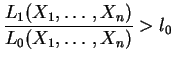 |
|||
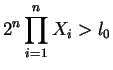 |
|||
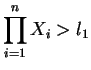 |
|||
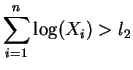 |
|||
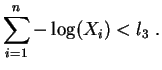 |
Pero si ![]() sigue la ley
sigue la ley
![]() (hipótesis
(hipótesis
![]() ), entonces
), entonces
![]() sigue la
ley exponencial
sigue la
ley exponencial
![]() , y como las
, y como las ![]() son independientes,
son independientes,
![]() sigue la
ley gamma
sigue la
ley gamma
![]() . La regla de decisión para el
test de
umbral
. La regla de decisión para el
test de
umbral ![]() es por tanto:
es por tanto:
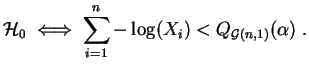
La ventaja del test del cociente de verosimilitud (cuando se puede construir explícitamente), es que él garantiza la mejor potencia posible, según el teorema de Neyman-Pearson :
Si ![]() denota el riesgo de segunda
especie del test del cociente de verosimilitud, y
denota el riesgo de segunda
especie del test del cociente de verosimilitud, y ![]() el de
cualquier otro test de las mismas hipótesis, decir que el test
del
cociente de verosimilitud es más potente que el otro quiere
decir que
el de
cualquier otro test de las mismas hipótesis, decir que el test
del
cociente de verosimilitud es más potente que el otro quiere
decir que ![]() es menor que
es menor que ![]() .
.