Estadística y probabilidades

Los tratamientos estadísticos se carácterizan por un ir y venir permanente entre los datos, que son colecciones de cifras medidas, y los modelos probabilistas que no tienen ninguna realidad física, pero proveen herramientas para describir la variabilidad de los datos. En esta manera de pensar, un primer paso consiste en asociar a la muestra una ley de probabilidad ficticia. La distribución empírica asociada a una muestra es la ley de probabilidad sobre el conjunto de las modalidades, que afecta a cada observación con el peso

. La idea es la siguiente. Supongamos que queremos aumentar artificialmente la cantidad de datos. La forma más simple sería sacar aleatoriamente nuevos valores a partir de los valores ya observados, respetando sus frecuencias. En otras palabras, se simularía la distribución empírica.

Definición 2.1 Sean $(x_1,\ldots,x_n)$ una muestra, $c_1,\ldots,c_k$ los diferentes valores que toman los

. Para $h=1,\ldots,k$ denotamos:

$\displaystyle n_h = \sum_{i=1}^n \mathbb {I}_{c_h}(x_i)\;,$

el número de veces que el valor

aparece o sea el efectivo del valor

. La distribución empírica de la muestra es la ley de probabilidad $\widehat{P}$ sobre el conjunto $\{c_1,\ldots,c_k\}$ , tal que:

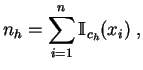
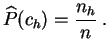
$\displaystyle \widehat{P}(c_h) = \frac{n_h}{n}\;.$

La media, la varianza y la desviación estándar pueden ser vistas como carácterísticas probabilistas de la distribución empírica. La media de la muestra es la esperanza de su distribución empírica.

Para un carácter discreto, la moda de la distribución empírica es el valor que tiene la frecuencia más alta. Para un carácter continuo agrupado en clases de amplitudes iguales, hablamos de clase modal. Una distribución empírica se llama unimodal si la frecuencia maximal es significativamente mayor que las otras. Puede ser bimodal o multimodal en otros casos.

Para estudiar una distribución empírica, la primera etapa consiste en ordenar los datos en orden creciente, es decir escribir sus estadígrafos de orden.

Definición 2.2 Sea $(x_1,\ldots,x_n)$ una muestra numérica. Llamamos estadígrafos de orden de la muestra, a los valores $x_{(1)},\ldots,x_{(n)}$ iguales a los

puestos en orden creciente:

$\displaystyle x_{(1)} = \min_{i=1,\ldots,n}\{x_i\}\leq x_{(2)}\leq\cdots\leq x_{(n)} = \max_{i=1,\ldots,n}\{x_i\}\;.$

Aquí tenemos como ejemplo a una muestra de tamaño

y sus

estadígrafos de orden.

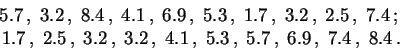
$\begin{displaymath} \begin{array}{c} 5.7\,,\;3.2\,,\;8.4\,,\;4.1\,,\;6.9\,,\; ... ...4.1\,,\; 5.3\,,\;5.7\,,\;6.9\,,\;7.4\,,\;8.4\,. \end{array} \end{displaymath}$

Definición 2.3 La función de distribución empírica es la función de $\mathbb {R}$ en

, que denotamos por $\widehat{F}$ y que toma los valores:

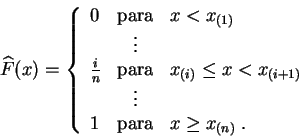
$\begin{displaymath} \widehat{F}(x) = \left\{ \begin{array}{lcl} 0 &\mbox{para... ...ts&\\ 1&\mbox{para}&x\geq x_{(n)}\;. \end{array} \right. \end{displaymath}$

En otras palabras, $\widehat{F}(x)$ es la proporción de los elementos de la muestra que son menores o iguales a