Sección : Estimación puntual
Previo : Intervalos de dispersión
Siguiente : Búsqueda de estimadores

Ejemplos de estimadores


En este parrafo, ilustramos las nociones de estimador, de consistencia y de sesgo a partir de tres ejemplos: la estimación de la varianza, el problema de las preguntas confidenciales y los conteos por captura-recaptura.

Estimadores de la varianza: Sea $ (X_1,\ldots,X_n)$ una muestra de una ley desconocida $ P$, suponiendo que admite momentos de todos los ordenes. Hemos visto que la media empírica $ \overline{X}_n=(X_1+\cdots+X_n)/n$ es un estimador consistente de la esperanza. Es un estimador insesgado y su varianza es igual a la varianza de la ley $ P$, dividida por $ n$. ¿Cómo estimar la varianza de $ P$? El estimador más natural es el siguiente.

Definición 1.11   Llamamos varianza empírica de la muestra $ (X_1,\ldots,X_n)$ al estimador:

$\displaystyle S^2_n = \frac{1}{n}\sum_{i=1}^n (X_i-\overline{X}_n)^2\;. $


Si $ X$ denota una variable aleatoria de ley $ P$, $ S^2_n$ es un estimador consistente de $ Var[X]=\mathbb {E}[(X-\mathbb {E}[X])^2]$, pero no es un estimador insesgado. En efecto:

Proposición 1.12  

$\displaystyle \mathbb {E}[S^2_n] = \frac{n-1}{n}Var[X]\;. $


Demostración: Calculemos primero $ \mathbb {E}[\overline{X}^2_n]$.

$\displaystyle \mathbb {E}[\overline{X}_n^2]$ $\displaystyle =$ $\displaystyle \frac{1}{n^2}\mathbb {E}[(X_1+\cdots+X_n)^2]$  
  $\displaystyle =$ $\displaystyle \frac{1}{n^2} \mathbb {E}\left[\sum_{i=1}^n X_i^2 + \sum_{i=1}^n\sum_{j\neq i} X_iX_j\right]\;.$  


Por definición de muestra, $ X_1,\ldots,X_n$ son independientes y de misma ley. Por tanto $ \mathbb {E}[X_i^2]=\mathbb {E}[X^2]$ y $ \mathbb {E}[X_iX_j]=(\mathbb {E}[X])^2$, donde $ X$ es una variable aleatoria cualquiera de ley $ P$. Sustituyendo estos valores obtenemos:

$\displaystyle \mathbb {E}[\overline{X}^2_n]$ $\displaystyle =$ $\displaystyle \frac{1}{n^2} \Big( n\mathbb {E}[X^2] + n(n-1) (\mathbb {E}[X])^2)\Big)$  
  $\displaystyle =$ $\displaystyle \frac{1}{n}\mathbb {E}[X^2] + \frac{n-1}{n} (\mathbb {E}[X])^2\;.$  

Tenemos, por tanto:
$\displaystyle \mathbb {E}[S^2_n]$ $\displaystyle =$ $\displaystyle \frac{1}{n}\mathbb {E}[X_1^2+\cdots+X_n^2]-\frac{1}{n}\mathbb {E}[X^2] - \frac{n-1}{n} (\mathbb {E}[X])^2)$  
  $\displaystyle =$ $\displaystyle \frac{n-1}{n}\mathbb {E}[X^2] - \frac{n-1}{n} (\mathbb {E}[X])^2)$  
  $\displaystyle =$ $\displaystyle \frac{n-1}{n}Var[X]\;.$  

$ \square$

Para transformar $ S^2_n$ en un estimador insesgado, es suficiente corregir el sesgo por un factor multiplicativo.

Definición 1.13   Se llama varianza empírica insesgada al estimador:

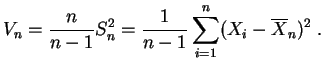
$\displaystyle V_n = \frac{n}{n-1} S^2_n = \frac{1}{n-1}\sum_{i=1}^n (X_i-\overline{X}_n)^2\;. $


Se puede estimar la desviación estándar por $ \sqrt{S^2_n}$ o por $ \sqrt{V_n}$. Notemos que en general tanto $ \sqrt{V_n}$ como $ \sqrt{S^2_n}$ son estimadores sesgados de $ \sqrt{Var[X]}$. La diferencia entre los dos estimadores tiende a 0, cuando el tamaño de la muestra tiende a infinito. No obstante, la mayor parte de las calculadoras proponen a los dos estimadores de la desviación estándar (teclas $ \sigma_n$ y $ \sigma_{n-1}$). Algunos logiciales (en particular Scilab) calculan el valor de $ V_n$ o $ \sqrt{V_n}$, otros calculan $ S^2_n$ o $ \sqrt{S^2_n}$. En lo que sigue emplearemos sobretodo a $ S^2_n$, a pesar del inconveniente del sesgo.

Preguntas confidenciales: Ciertos temas abordados en las encuestas de opinión son bastante íntimos y se corre el riesgo que las personas encuestadas rehuyan responder francamente al encuestador, falseando así el resultado. Podemos entonces recurrir a una astucia que consiste en invertir aleatoriamente las respuestas. Consideremos una pregunta confidencial para la cual queremos estimar la probabilidad $ p$ de respuestas positivas. El encuestador pide a cada persona encuestada de lanzar un dado. Si en el dado sale $ 6$, la persona debe responder sin mentir, si no, debe dar la opinión contraria a la suya. Si el encuestador ignora cuanto salió en el dado, no podrá saber si la respuesta es veraz o no, y se puede esperar que la persona encuestada aceptará jugar el juego. Generalicemos ligeramente la situación sacando, para cada persona, una variable de Bernoulli de parámetro $ \alpha$. Si el resultado de esta variable es $ 1$, la respuesta es veraz, si no, se invierte la respuesta. Sea $ n$ el número de personas encuestadas. El encuestador recoge solamente la frecuencia empírica $ F_n$ de los ''sí''. La proporción desconocida de los ''sí'' a partir de este procedimiento es $ q=\alpha p + (1-\alpha)(1-p)$ y la frecuencia $ F_n$ observada por el encuestador es un estimador insesgado y consistente de $ q$. Observemos que si $ \alpha=1/2$, $ q$ vale $ 1/2$, cualquiera que sea $ p$. Pero si $ \alpha\neq 1/2$, podemos expresar $ p$ en función de $ q$:

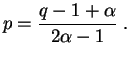
$\displaystyle p=\frac{q-1+\alpha}{2\alpha-1}\;. $


Por tanto podemos proponer como estimador de $ p$ a la cantidad siguiente:

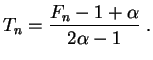
$\displaystyle T_n=\frac{F_n-1+\alpha}{2\alpha-1}\;. $

La esperanza de $ T_n$ es $ p$. La varianza de $ T_n$ vale:

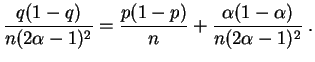
$\displaystyle \frac{q(1-q)}{n(2\alpha-1)^2} = \frac{p(1-p)}{n} + \frac{\alpha(1-\alpha)}{n(2\alpha-1)^2}\;. $


El estimador $ T_n$ es insesgado y su varianza tiende a 0, por lo tanto es consistente.

Para $ n$ fijo, la varianza de $ T$ tiende a infinito cuando $ \alpha$ tiende a $ 1/2$. Ella es minimal si $ \alpha=0$ o $ 1$ (pero entonces el procedimiento pierde todo su interés). El problema consiste entonces en seleccionar un valor de $ \alpha$ que sea bastante grande, para que la confidencialidad sea creíble, pero lo suficientemente alejado de $ 1/2$ para no aumentar demasiado la varianza del estimador. Para el dado, el valor de $ \alpha$ es $ 1/6$ y el término adicional de la varianza es proporcional a $ \alpha(1-\alpha)/(2\alpha-1)^2 = 0.3125$.

Conteos por captura-recaptura: ¿Cómo estimar el número de especies de insectos que viven en la Tierra, ya que numerosas especies son, todavía, desconocidas? ¿Cómo conocemos la población de ballenas en el océano? El conteo por captura-recaptura permite evaluar las poblaciones para las cuales un censo exhaustivo es imposible. El método se basa en una idea simple. Consideremos una población de tamaño $ N$, desconocido. Se toma, en un primer momento, un grupo de individuos de tamaño $ m$ fijo. Estos individuos son censados y marcados de manera tal que puedan ser reconocidos posteriormente. Más tarde, se toma un nuevo grupo de tamaño $ n$ y observamos el número $ X$ de individuos marcados en este nuevo grupo. Si el segundo muestreo es independiente del primero, la ley de $ X$ es la ley hipergeométrica de parámetros $ N$, $ m$ y $ n$, de esperanza $ nm/N$. Podemos esperar que la proporción de individuos marcados en el segundo grupo esté cercano de la proporción de individuos marcados en el total de la población, $ m/N$. Por tanto es razonable proponer como estimador de $ N$ a la cantidad siguiente:

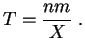
$\displaystyle T=\frac{nm}{X}\;. $


El inconveniente de este estimador es que no está definido si $ X$ toma el valor 0, lo que sucede con una probabilidad estrictamente positiva. Se puede corregir este defecto de dos maneras. La primera consiste en reemplazar $ X$ por $ X+1$, lo cual no debería falsear mucho los resultados, si los números con que trabajamos son bastante grandes. Pongamos entonces:

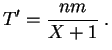
$\displaystyle T'=\frac{nm}{X+1}\;. $


La segunda manera consiste en decidir de rechazar a priori las muestras para las cuales no se obtengan individuos marcados. Esto significa reemplazar a $ X$ por otra variable aleatoria $ X'$ cuya ley es la ley condicional de $ X$ sabiendo que $ X$ es estrictamente positiva. Pongamos entonces:

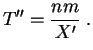
$\displaystyle T'' = \frac{nm}{X'}\;. $


Para valores de $ N$, $ m$ y $ n$ específicos, podemos calcular numéricamente las esperanzas y las desviaciones estándar de estos estimadores. La tabla que mostramos a continuación resume los resultados obtenidos para $ m=n=100$ y diferentes valores de $ N$.

$ N$
200
300
400
500
1000
5000
$ \mathbb {E}[T']$
197.0
295.1
393.1
491.1
981.3
4291.1
$ \sqrt{Var[T']}$
13.9
34.4
60.2
90.7
309.3
2459.5
$ \mathbb {E}[T'']$
201.0
304.2
409.6
517.5
1102.0
5767.9
$ \sqrt{Var[T'']}$
14.5
36.6
65.6
101.5
420.2
2995.4

Los dos estimadores son sesgados, el primero tiene tendencia a subestimar el tamaño $ N$ de la población, el segundo a sobreestimarlo. La desviación estándar aumenta más rápidamente que $ N$. Es natural que la precisión relativa sea más débil según que las muestras recogidas sean pequeñas con respecto al tamaño desconocido de la población.


Sección : Estimación puntual
Previo : Intervalos de dispersión
Siguiente : Búsqueda de estimadores