Sección : Estimación paramétrica
Previo : Normalidad asintótica
Siguiente : Índice
NB: En los ejercicios que siguen, los valores
propuestos para los tamaños de las muestras así como para los
parámetros de las leyes, son solamente indicativos. Pueden ser
variados en función de la potencia de cálculo disponible.
Ejercicio 18
- En un número
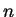 desconocido de lanzamientos de una moneda
equilibrada se obtuvieron 6 caras. Proponer un intervalo de
confianza de nivel
desconocido de lanzamientos de una moneda
equilibrada se obtuvieron 6 caras. Proponer un intervalo de
confianza de nivel 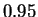 para
para 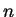 .
.
- En una muestra de tamaño
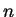 desconocido de la ley de Poisson
desconocido de la ley de Poisson
 , la suma de
los valores es
, la suma de
los valores es 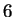 . Proponer un un intervalo de confianza de nivel
. Proponer un un intervalo de confianza de nivel
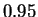 para
para 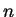 .
.
Ejercicio 19
Se considera el modelo lineal

, donde

sigue la ley
normal

. Escribir un programa que
toma como entrada un vector

, valores de
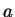
,
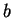
,
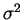
,
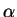
y
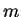
, y realiza las operaciones siguientes.
- Simular una muestra
 , del mismo tamaño que
, del mismo tamaño que 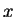 , de
la ley
, de
la ley
 .
.
- Calcular el vector
 .
.
- Calcular los coeficientes
 y
y
 de la recta de regresión lineal de
de la recta de regresión lineal de  sobre
sobre 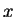 ,
así como el error cuadrático minimal
,
así como el error cuadrático minimal
 .
.
- Calcular los intervalos de confianza de nivel
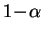 para
para 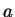 ,
, 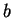 y
y 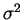 .
.
- Calcular, para un
vector
 de valores regularmente distribuidos entre
de valores regularmente distribuidos entre
 y
y
 , los vectores
, los vectores
 y
y
 de los extremos de los intervalos
de predicción de nivel
de los extremos de los intervalos
de predicción de nivel
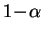 para
para
 .
.
- Representar en un mismo gráfico los puntos de coordenadas
 , la recta de regresión lineal de
, la recta de regresión lineal de  sobre
sobre 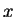 , los
puntos de coordenadas
, los
puntos de coordenadas
 y
y
 .
.
Ejecutar el programa para

,

,

,

,

, y los vectores
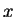
de longitud 100 definidos
a continuación.
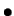
- Valores distribuidos regularmente entre 0 y 10.
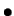
- Valores distribuidos regularmente entre 0 y 1.
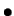
- Valores simulados a partir de la ley normal
 .
.
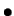
- Valores simulados a partir de
la ley normal
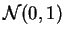 .
.
- Valores simulados
a partir de la ley exponencial
 .
.
Ejercicio 21
- Para
 , simular una muestra de tamaño
, simular una muestra de tamaño
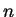 de la ley normal
de la ley normal
 .
.
- Suponiendo
desconocida la varianza, calcular el intervalo de confianza exacto
de nivel
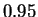 para la esperanza. Calcular el intervalo de
confianza de nivel asintótico
para la esperanza. Calcular el intervalo de
confianza de nivel asintótico 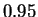 . Comparar los dos intervalos.
. Comparar los dos intervalos.
- Calcular el intervalo de confianza optimal de nivel
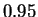 para la varianza. Calcular el intervalo de confianza de nivel
asintótico
para la varianza. Calcular el intervalo de confianza de nivel
asintótico 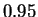 , obtenido al reemplazar la ley de chi-cuadrado
por la ley normal de la misma esperanza y la misma varianza.
Comparar los dos intervalos.
, obtenido al reemplazar la ley de chi-cuadrado
por la ley normal de la misma esperanza y la misma varianza.
Comparar los dos intervalos.
Sección : Estimación paramétrica
Previo : Normalidad asintótica
Siguiente : Índice
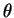 . Calcular, cuando sea posible, sus sesgos y sus
errores cuadráticos con respecto a
. Calcular, cuando sea posible, sus sesgos y sus
errores cuadráticos con respecto a 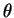 .
.
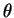 y simular 1000 muestras de tamaño 100 de la
ley
y simular 1000 muestras de tamaño 100 de la
ley
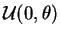 . Calcular para cada una de estas muestras
el valor que toman los 10 estimadores. Calcular la media empírica,
y la varianza empírica de las 10 muestras de tamaño 1000 que se
obtuvieron. A partir de esto deducir una estimación del sesgo y
del error cuadrático de cada uno de los 10 estimadores.
. Calcular para cada una de estas muestras
el valor que toman los 10 estimadores. Calcular la media empírica,
y la varianza empírica de las 10 muestras de tamaño 1000 que se
obtuvieron. A partir de esto deducir una estimación del sesgo y
del error cuadrático de cada uno de los 10 estimadores.
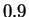 .
.













