La modelación probabilista en
estadística consiste en suponer que una muestra observada
![]() es una realización de una muestra teórica de
una cierta ley de probabilidad
es una realización de una muestra teórica de
una cierta ley de probabilidad ![]() , donde el parámetro
, donde el parámetro
![]() es desconocido. Si este es el caso, la
distribución
empírica
es desconocido. Si este es el caso, la
distribución
empírica
![]() de la muestra observada debería estar
cerca de
de la muestra observada debería estar
cerca de ![]() . La distribución empírica de una muestra es la
ley de probabilidad sobre el conjunto de los valores, que afecta a
cada individuo con el peso
. La distribución empírica de una muestra es la
ley de probabilidad sobre el conjunto de los valores, que afecta a
cada individuo con el peso ![]() .
.
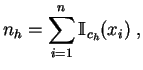
el número de veces que el valor ![]() aparece o sea el efectivo
del valor
aparece o sea el efectivo
del valor ![]() . La distribución empírica de
la muestra es la ley de probabilidad
. La distribución empírica de
la muestra es la ley de probabilidad
![]() sobre el
conjunto
sobre el
conjunto
![]() , tal que:
, tal que:
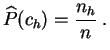
Entre las diferentes formas de cuantificar el ajuste de una distribución empírica a una ley de probabilidad teórica, trataremos dos: la distancia de chi-cuadrado (para las leyes discretas) y la distancia de Kolmogorov-Smirnov.
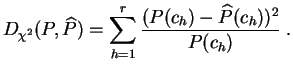
La
distancia de Kolmogorov-Smirnov es la distancia de la norma
uniforme entre funciones de
distribución. Recordemos que la
función de distribución empírica
de la muestra
![]() es la función de distribución de
su distribución empírica. Es la función en escalera
es la función de distribución de
su distribución empírica. Es la función en escalera
![]() que vale 0 antes de
que vale 0 antes de ![]() ,
, ![]() entre
entre ![]() y
y
![]() , y
, y ![]() después de
después de ![]() , donde los
, donde los ![]() son
los
estadígrafos de orden, es decir los valores de
la muestra ordenados.
son
los
estadígrafos de orden, es decir los valores de
la muestra ordenados.
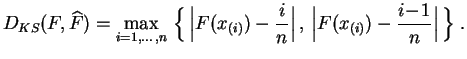
Dados una muestra y una familia de leyes de probabilidad
![]() , que dependen de un parámetro desconocido
, que dependen de un parámetro desconocido ![]() , es
natural seleccionar como modelo a la ley de la familia que se
ajusta mejor a los datos. Esto se convierte en tomar como
estimación de
, es
natural seleccionar como modelo a la ley de la familia que se
ajusta mejor a los datos. Esto se convierte en tomar como
estimación de ![]() aquel para el cual la distancia entre la
ley teórica
aquel para el cual la distancia entre la
ley teórica ![]() y la distribución empírica de la muestra
sea menor.
y la distribución empírica de la muestra
sea menor.
Consideremos, por ejemplo, una muestra de datos binarios.
Denotemos por ![]() la
frecuencia
empírica de los 1. La
distancia de
chi-cuadrado entre la
ley de Bernoulli de parámetro
la
frecuencia
empírica de los 1. La
distancia de
chi-cuadrado entre la
ley de Bernoulli de parámetro ![]() y la
distribución empírica es:
y la
distribución empírica es:
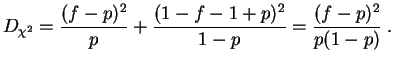
Esta distancia es evidentemente mínima para ![]() . Esto puede
extenderse de manera evidente a un número finito cualquiera de
eventualidades: la ley de probabilidad que mejor se ajusta a una
distribución empírica sobre
. Esto puede
extenderse de manera evidente a un número finito cualquiera de
eventualidades: la ley de probabilidad que mejor se ajusta a una
distribución empírica sobre
![]() , en el sentido de la
distancia chi-cuadrado, es aquella que asigna a cada valor
, en el sentido de la
distancia chi-cuadrado, es aquella que asigna a cada valor ![]() una probabilidad igual a la frecuencia experimental de este valor.
una probabilidad igual a la frecuencia experimental de este valor.
En la práctica es raro que se pueda calcular explícitamente la estimación de un parámetro por ajuste. Se debe proceder a una minimización numérica sobre el parámetro desconocido.