Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit
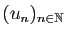 une suite de réels.
une suite de réels.
- Quand dit-on que la suite
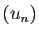 est croissante à partir d'un
certain rang ?
est croissante à partir d'un
certain rang ?
- Quand dit-on que la suite
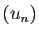 est majorée ?
est majorée ?
- Quand dit-on que la suite
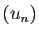 tend vers
tend vers 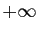 ?
?
- Démontrer que si la suite
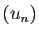 est majorée à partir d'un
certain rang, alors elle est majorée.
est majorée à partir d'un
certain rang, alors elle est majorée.
- Démontrer que si la suite
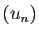 est croissante à partir d'un
certain rang, et non majorée, alors elle tend vers
est croissante à partir d'un
certain rang, et non majorée, alors elle tend vers 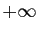 .
.
Exercice 1 :
Dans tout l'exercice, 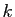 désigne un entier strictement positif,
et
désigne un entier strictement positif,
et 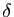 un réel tel que
un réel tel que
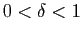 .
.
- Démontrer que
- En déduire que la suite
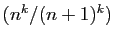 est minorée par
est minorée par
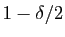 , à partir d'un certain rang.
, à partir d'un certain rang.
- Pour tout
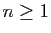 , on pose :
, on pose :
Montrer que la suite
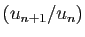 est minorée par
est minorée par
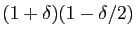 à partir d'un certain rang. En déduire
que la suite
à partir d'un certain rang. En déduire
que la suite 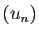 tend vers
tend vers 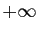 .
.
- Démontrer que pour tous réels
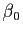 ,
, 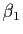 tels que
tels que
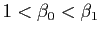 ,
,
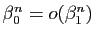 .
.
- Déduire des questions précédentes que pour tout
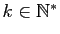 ,
et pour tout
,
et pour tout 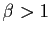 ,
,
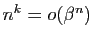 .
.
- Démontrer les relations de comparaison suivantes.
Exercice 2 :
On considère la suite 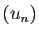 définie par
définie par
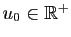 et pour tout
et pour tout
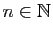 ,
,
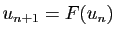 , avec :
, avec :
- Montrer que le seul point fixe de
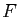 est
est 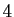 .
.
- Représenter le graphe de
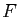 . Utiliser les diagrammes en toile
d'araignée pour deviner le comportement de la suite
. Utiliser les diagrammes en toile
d'araignée pour deviner le comportement de la suite 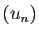 pour
pour
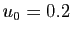 , et
, et 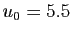 .
.
- Montrer que pour tout
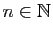 ,
,
- Montrer que si
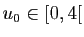 , alors pour tout
, alors pour tout 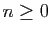 ,
,
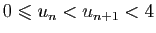 .
.
- En déduire que si
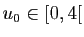 , alors la suite
, alors la suite 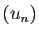 converge
vers
converge
vers 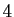 .
.
- Montrer que si
![$ u_0\in]4+\infty[$](img583.gif) , alors pour tout
, alors pour tout 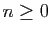 ,
,
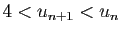 .
.
- En déduire que si
![$ u_0\in]4,+\infty[$](img585.gif) , alors la suite
, alors la suite 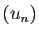 converge
vers
converge
vers 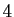 .
.
- Démontrer que pour tout
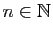 ,
,
- En déduire que
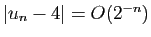 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() une suite de réels.
une suite de réels.
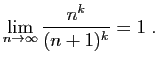
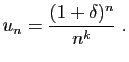
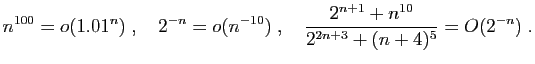
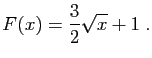
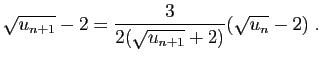
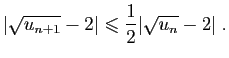
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales