On étend aux suites à valeurs dans
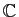 toutes les propriétés
des suites de réels, sauf celles qui font référence à
l'ordre. On
ne parle pas de suite complexe croissante, décroissante, majorée
ou minorée, car contrairement à
toutes les propriétés
des suites de réels, sauf celles qui font référence à
l'ordre. On
ne parle pas de suite complexe croissante, décroissante, majorée
ou minorée, car contrairement à
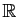 ,
,
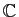 n'est pas
naturellement muni d'une relation d'ordre.
Pour les propriétés où la distance
n'est pas
naturellement muni d'une relation d'ordre.
Pour les propriétés où la distance 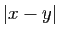 intervient, la valeur absolue est remplacée par le module, qui se
note de la même façon.
Par exemple une suite
intervient, la valeur absolue est remplacée par le module, qui se
note de la même façon.
Par exemple une suite 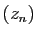 est bornée si pour tout
est bornée si pour tout
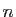 ,
,
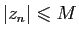 . Elle converge vers
. Elle converge vers
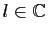 si
si
qu'il faut comprendre comme «tous les termes de la suite restent dans
un disque de rayon
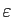 autour de la limite à partir d'un certain
rang» (voir la figure 3 pour une illustration).
autour de la limite à partir d'un certain
rang» (voir la figure 3 pour une illustration).
Figure 3:
Convergence dans
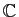 de la suite
de la suite
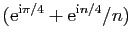 .
.
|
|
Le théorème suivant montre que la convergence d'une suite
de complexes équivaut à la convergence de sa partie réelle et de sa
partie imaginaire.
Démonstration : Elle est essentiellement basée sur l'encadrement suivant entre le
module d'un nombre complexe et les valeurs absolues des parties
réelle et imaginaire. Soit
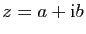 un complexe, alors
un complexe, alors
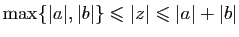 |
(1) |
On note 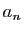 et
et 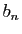 la partie réelle et la partie imaginaire de
la partie réelle et la partie imaginaire de 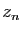 .
Si
.
Si 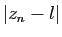 reste inférieur à
reste inférieur à
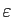 , alors il en est de même
pour
, alors il en est de même
pour
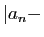 Re
Re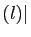 et
et
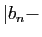 Im
Im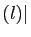 , par la première
inégalité de (1). Réciproquement, si
, par la première
inégalité de (1). Réciproquement, si
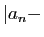 Re
Re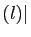 et
et
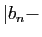 Im
Im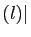 sont inférieurs à
sont inférieurs à
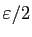 , alors
, alors 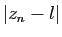 est inférieur à
est inférieur à
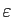 , par la seconde
inégalité de (1).
, par la seconde
inégalité de (1).
Posons par exemple
Les parties réelle et imaginaire sont :
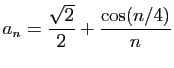
et
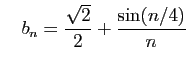
Les deux suites convergent vers
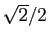 , et
, et 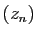 converge
vers
converge
vers
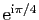 . La figure 3 représente dans le plan
complexe les
. La figure 3 représente dans le plan
complexe les 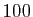 premiers termes de la suite
premiers termes de la suite 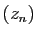 , ainsi que le
cercle de rayon
, ainsi que le
cercle de rayon
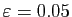 centré en
centré en
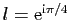 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() toutes les propriétés
des suites de réels, sauf celles qui font référence à
l'ordre. On
ne parle pas de suite complexe croissante, décroissante, majorée
ou minorée, car contrairement à
toutes les propriétés
des suites de réels, sauf celles qui font référence à
l'ordre. On
ne parle pas de suite complexe croissante, décroissante, majorée
ou minorée, car contrairement à
![]() ,
,
![]() n'est pas
naturellement muni d'une relation d'ordre.
Pour les propriétés où la distance
n'est pas
naturellement muni d'une relation d'ordre.
Pour les propriétés où la distance ![]() intervient, la valeur absolue est remplacée par le module, qui se
note de la même façon.
Par exemple une suite
intervient, la valeur absolue est remplacée par le module, qui se
note de la même façon.
Par exemple une suite ![]() est bornée si pour tout
est bornée si pour tout
![]() ,
,
![]() . Elle converge vers
. Elle converge vers
![]() si
si
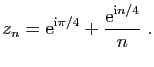
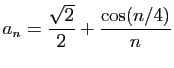 et
et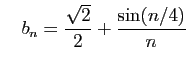
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales