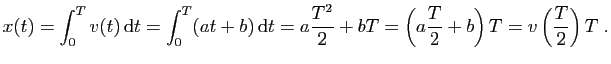
Cette sorte de mouvement appartient en propre aux choses qui se meuvent naturellement et aux projectiles. Car lorsqu'un corps tombe dans un milieu homogène, il se déplace plus rapidement à la fin qu'au début. D'un autre côté, le mouvement des projectiles vers le haut est moins rapide à la fin qu'au début. De sorte que le premier croît uniformément, tandis que le second décroît uniformément.Eh oui : le «théorème de Merton» décrivait la loi de la chute des corps..., publiée par Galilée presque 3 siècles après les calculateurs d'Oxford, et qui lui est attribuée depuis. Voici comment Galilée l'énonce en 1632.
Le temps dans lequel une certaine distance est parcourue par un mobile uniformément accéléré à partir du repos est égal au temps dans lequel la même distance serait parcourue par le même corps voyageant avec une vitesse uniforme, égale à la moitié de la vitesse maximale finale du mouvement uniformément accéléré original.Parmi les calculateurs d'Oxford, Richard Swineshead, dont le nom avait été déformé en Suiseth, ou Suisset, a suscité l'admiration de ses successeurs. Cardan l'avait classé parmi les 10 plus grands esprits de tous les temps. Leibniz, qui s'était procuré une copie de son manuscrit, écrivait en 1714: «Il y a eu autrefois un Suisse, qui avoit mathématisé dans la Scholastique : ses ouvrages sont peu connus ; mais ce que j'en ai vu m'a paru profond et considérable». Qu'y avait-il de si profond dans le liber calculationum de Swineshead ? Entre autres plusieurs démonstrations du théorème de Merton. Dans l'une d'elles, l'étape principale consiste à montrer que pour un mouvement uniformément décéléré jusqu'à l'arrêt complet, la distance parcourue pendant la première moitié du temps est le triple de la distance parcourue dans la seconde moitié. Voici ce que dit Swineshead.
Pour cela, supposons queEn notations modernes, soitdécélère uniformément jusqu'à zéro. Alors dans chacun des instants de la première partie proportionnelle du temps, il ira deux fois plus vite que dans la partie correspondante de la seconde partie, et ainsi de suite pour les parties suivantes, comme il est évident. Comme la première partie proportionnelle du temps est le double de la seconde, il est évident que
parcoura quatre fois plus de distance dans la première que dans la seconde, dans la seconde que dans la troisième, et ainsi jusqu'à l'infini.
![$\displaystyle I_n=\left]\frac{(2^{n}-1)T}{2^{n}},\frac{(2^{n+1}-1)T}{2^{n+1}}\right]\;.$](img798.gif)
La conséquence découle du fait que si deux ensembles de quantités sont comparés terme à terme de sorte que chaque comparaison donne la même proportion, alors, si la somme du premier ensemble est comparée avec la somme des termes du second ensemble, les sommes auront la même proportion que celle des comparaisons terme à terme des deux ensembles.Traduisez :
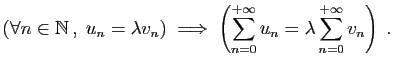
Il s'ensuit donc que dans l'intervalle de temps complet,Vous vous demandez pourquoi avoir eu recours à une sommation de série, alors qu'il suffisait d'appliquer l'argument à la deuxième moitié (un quart de la distance totale parcourue, puisque la durée et la vitesse sont la moitié) ? Moi aussi. Peut-être par fidélité à Aristote et son paradoxe de dichotomie. En tout cas, le même genre d'argument lui permettait d'aller encore plus loin.parcourra quatre fois plus d'espace que dans la seconde moitié du temps. Donc dans la première moitié du temps, il traversera trois fois autant d'espace que dans la seconde moitié.
Si un point se meut à une vitesse constante durant la première moitié d'un intervalle de temps, durant le quart suivant de l'intervalle de temps à une vitesse double de la vitesse initiale, durant le huitième suivant de l'intervalle à une vitesse triple, etc. ad infinitum ; alors la vitesse moyenne durant l'intervalle de temps total sera le double de la vitesse initiale.En d'autres termes :
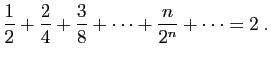
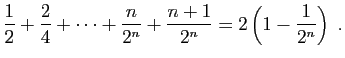
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales