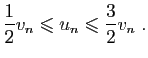
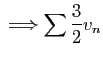 converge
converge
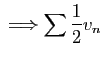 diverge
diverge
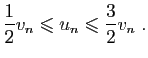
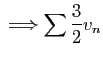 converge
converge
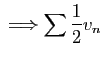 diverge
diverge
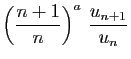 |
|||
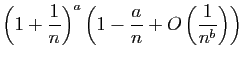 |
|||
 |
|||
 |
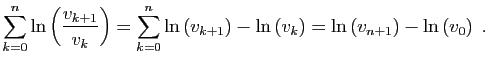
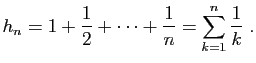
![$\displaystyle \forall t\in [k,k+1]\;,\quad
\frac{1}{k+1}\;\leqslant\; \frac{1}{t}\;\leqslant\; \frac{1}{k}\;.
$](img706.gif)
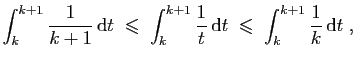
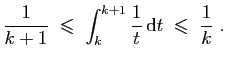
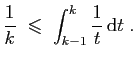
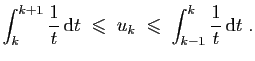
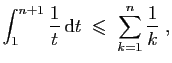
Sommons ensuite la seconde inégalité, pour ![]() allant de
allant de ![]() à
à
![]() :
:
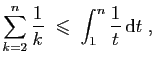
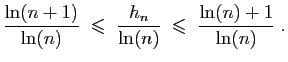
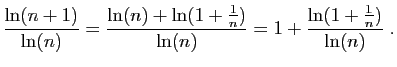
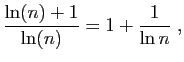
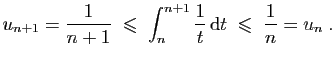
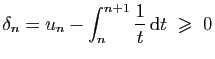 et
et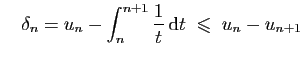
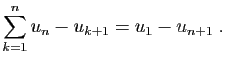
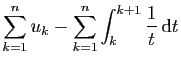 |
|||
 |
|||
 |
|||
 |
![$\displaystyle \int_0^1 t^{k-1} \mathrm{d}t = \left[ \frac{t^k}{k}\right]_0^1 = \frac{1}{k}\;.
$](img739.gif)
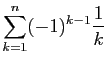 |
|||
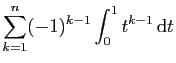 |
|||
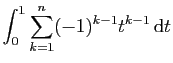 |
|||
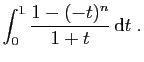 |
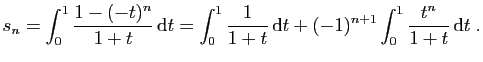
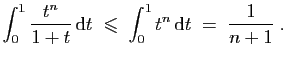

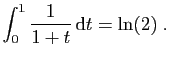
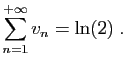
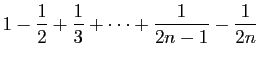 |
|||
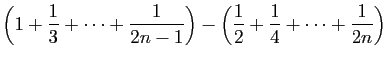 |
|||
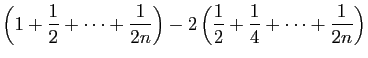 |
|||
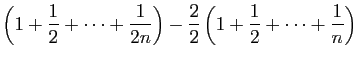 |
|||
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales