Les grands systèmes

Même si aucun des systèmes résolus dans le cours ne dépassait 4 inconnues, on demande couramment aux ordinateurs de résoudre des systèmes à plusieurs millions d'inconnues. D'où viennent-ils ?

La physique fournit toute une famille d'équations différentielles ou d'équations aux dérivées partielles qui décrivent avec une précision étonnante les phénomènes auxquels elles s'appliquent : équation de Maxwell, de Schrödinger, d'Euler, de Navier-Stokes...  À titre d'exemple, voici la plus célèbre des équations aux dérivées partielles, l'équation de la chaleur. Considérons un corps homogène dans l'espace, et notons $f(t,x,y,z)$ la température au temps $t$ du point de coordonnées $(x,y,z)$. L'application $f$ est solution de l'équation aux dérivées partielles suivante :

$$\frac{\partial f}{\partial t} = \frac{\lambda}{\rho C_p}\left(\f... ...frac{\partial^2 f}{\partial y^2} +\frac{\partial^2 f}{\partial z^2}\right) \;.$$

où $\lambda$ est la conductivité thermique, $\rho$ la masse volumique et $C_p$ la chaleur spécifique. L'application suivante porte le nom de «noyau de la chaleur»  car elle est solution de l'équation de la chaleur, ce qui se vérifie facilement.

$$f(t,x,y,z) = \frac{1}{t\sqrt{t}}\exp\left(-\frac{c}{t}(x^2+y^2+z^2)\right)\;,$$

où $c=\frac{\rho C_p}{4\lambda}$.

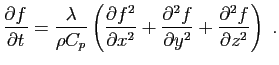
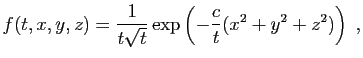
Il est extrêmement rare qu'une équation différentielle admette une solution explicite comme celle-ci, et quand c'est le cas, la solution trouvée correspond à des conditions qui ne sont pas physiquement réalistes. Il n'y a en général pas d'autre recours que de résoudre l'équation de manière approchée par un algorithme de discrétisation. L'idée consiste à approcher les dérivées de la fonction inconnue par ses accroissements sur un pas de discrétisation, choisi suffisamment petit.

Pour être plus précis, nous allons prendre comme exemple l'équation de la chaleur en dimension 1. Considérons une tige homogène, et notons $f(t,x)$ sa température à l'instant $t$ et à l'abscisse $x$.

$$\frac{\partial f}{\partial t} = \frac{\lambda}{\rho C_p} \frac{\partial^2 f}{\partial x^2}\;.$$

Choisissons un pas de temps $\delta t$ et un pas d'espace $\delta x$ (petits). À l'instant $t$, nous approchons la dérivée partielle en temps par le taux d'accroissement sur un intervalle de longueur $\delta t$ :

$$\frac{\partial f}{\partial t}\simeq \frac{1}{\delta t} \Big(f(t+\delta t,x)-f(t,x)\Big)\;.$$

De même la dérivée partielle seconde en espace est approchée par une différence d'accroissements, soit :

$$\frac{\partial f^2}{\partial x^2} \simeq \frac{1}{(\delta x)^2}\Big((f(t,x+\delta x)-2f(t,x)+f(t,x-\delta x)\Big)\;.$$

On ne conserve que les instants et les abscisses qui sont des multiples entiers de $\delta t$ et $\delta x$. Posons donc, pour tout couple d'entiers $i,j$,

$$f_{i,j} = f(i\delta t,j\delta x)\;.$$

L'équation de la chaleur est remplacée par un système linéaire d'équations reliant entre elles les inconnues $f_{i,j}$ :

$$\frac{1}{\delta t}\Big(f_{i+1,j}-f_{i,j}\Big) = \frac{\lambda}{\rho C_p} \frac{1}{(\delta x)^2} \Big(f_{i+1,j}-2f_{i,j}+f_{i-1,j}\Big)\;.$$

Pour arriver à un système lisible, simplifions encore. Prenons une barre en équilibre thermique, dont la température est fixée à $a$ à l'abscisse 0 et $b$ à l'abscisse $(n+1)\delta x$, Calculons sa température à l'abscisse $i\delta x$, pour $i=1,\ldots,n$. Puisque l'équilibre thermique est atteint, nous cherchons une fonction constante en temps, c'est-à-dire telle que $\partial f/\partial t=0$. Notons $f_i$ la valeur approchée de la température au point $i\delta x$ de la barre. Le système dont les $f_i$ sont solution est le suivant.

$$\left\{ \begin{array}{lcl} \hspace{16mm}2f_1-f_2&=&a\\ &\vd... ..._{i+1}&=&0\\ &\vdots&\\ -f_{n-1}+2f_n&=&b \end{array}\right.$$

Nous laissons au lecteur le soin de vérifier que ce système admet une solution unique, définie pour $i=1,\ldots,n$ par

$$f_i = a+(b-a)\frac{i}{n+1}\;.$$

Ceci correspond bien au fait qu'une fonction telle que $f''(x)=0$ est un polynôme de degré 1 : $f(x)=\alpha x+\beta$.

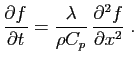
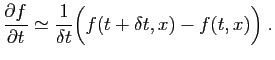
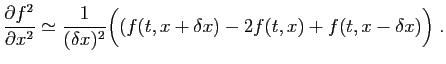
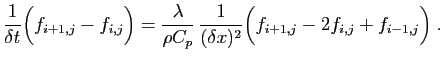
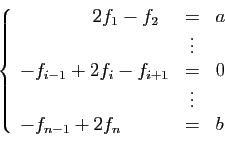
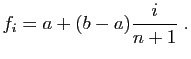
Chacune des équations du système ci-dessus contient relativement peu de termes non nuls : on dit que le système est creux. C'est le cas en général pour les systèmes obtenus après discrétisation d'un problème différentiel. Ceci facilite le stockage en mémoire, et accélère la résolution, grâce à la mise au point d'algorithmes adaptés. Il reste ensuite à démontrer que la solution du système linéaire approche bien la solution du problème différentiel, en un sens qu'il faudrait préciser. Ceci fait l'objet de théorèmes de convergence que nous n'aborderons pas.

Figure 6: Exemple de maillage.

L'équilibre thermique d'une barre n'a évidemment que peu d'intérêt pratique. Pour un bâtiment en construction, prévoir la puissance de la chaufferie et calculer la consommation d'énergie sont des problèmes nettement plus concrets. Or les volumes à chauffer ont 3 dimensions. Pour peu qu'on souhaite 100 pas de discrétisation dans chacune des trois dimensions, on arrive à un système certes linéaire, mais qui a déjà un million d'inconnues. Des moyens de découper l'espace plus astucieusement que par des petits cubes ont été inventés. On les appelle des maillages. Vous en voyez parfois dans les «making of»  des films d'animation, où ils sont utilisés pour rendre les mouvements plus réalistes. Vous les voyez aussi sur des présentations de voitures ou d'avions : ils sont utilisés pour calculer par l'équation de Navier-Stokes l'écoulement de l'air autour de la carrosserie, et donc prédire la portance de l'avion ou la consommation de la voiture.