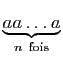 si
si
Rappelons une définition déjà utilisée en partie.
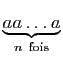 si
si
Définition équivalente (évitant
l'emploi des trois petits points)
On définit par
récurrence ![]() pour tout entier
pour tout entier ![]() positif ou
nul en posant
positif ou
nul en posant ![]() puis, pour tout
puis, pour tout
![]() ,
,
![]() ,
puis on définit directement
,
puis on définit directement ![]() pour tout
entier
pour tout
entier ![]() négatif en posant
négatif en posant
![]() (puisque
(puisque ![]() est alors déjà défini).
est alors déjà défini).
Démonstration : C'est très simple à voir avec des points de suspension, en
n'oubliant pas de distinguer plein de cas selon les signes des divers entiers
des formules, la définition dépendant de ce signe.
Comme c'est à la fois très
facile et très fastidieux, on va oublier discrètement de le faire.![]()
On en déduit aussitôt la très élémentaire
Démonstration : L'ensemble
![]() n'est pas vide, puisqu'il contient
n'est pas vide, puisqu'il contient
![]() . Si
. Si ![]() et
et ![]() sont deux éléments de
sont deux éléments de
![]() , on peut trouver deux
entiers (relatifs)
, on peut trouver deux
entiers (relatifs) ![]() et
et ![]() permettant d'écrire
permettant d'écrire ![]() et
et
![]() . Dès lors
. Dès lors
![]() et donc
et donc
![]() appartient à
appartient à
![]() .
.![]()
Afin de tenter de prévenir les confusions, introduisons un autre sens du mot «ordre», pas du tout synonyme du précédent et un peu superflu mais tellement passé dans les usages qu'on ne peut l'éviter.
Histoire d'appliquer rétroactivement la division euclidienne, qui sera correctement définie dans le chapitre sur l'arithmétique, démontrons le
Démonstration : La preuve étant plus longue que la moyenne, essayons de
dégager des étapes
intermédiaires avec des énoncés précis, qui nous
permettront de souffler quand
ils seront atteints. On notera ![]() l'élément neutre
du groupe considéré.
l'élément neutre
du groupe considéré.
Étape intermédiaire 1 : si l'ordre de ![]() est fini, noté
est fini, noté ![]() ,
,
Preuve de l'étape 1. Soit ![]() un élément de
un élément de
![]() , c'est-à-dire une puissance de
, c'est-à-dire une puissance de ![]() . On peut
donc mettre
. On peut
donc mettre ![]() sous forme
sous forme ![]() pour un entier relatif
pour un entier relatif ![]() .
Effectuons la division euclidienne de
.
Effectuons la division euclidienne de ![]() par
par ![]() , ainsi
, ainsi ![]() ,
avec
,
avec
![]() . On a alors
. On a alors
Étape intermédiaire 2 : si l'ordre de ![]() est fini,
le théorème est vrai.
est fini,
le théorème est vrai.
Preuve de l'étape 2. Notons ![]() l'ordre de
l'ordre de ![]() . Il découle du
résultat de l'étape 1 que dans cette hypothèse
l'ensemble
. Il découle du
résultat de l'étape 1 que dans cette hypothèse
l'ensemble
![]() possède au plus
possède au plus ![]() éléments. L'étudiant
distrait croira même qu'on a
déjà prouvé qu'il en possède exactement
éléments. L'étudiant
distrait croira même qu'on a
déjà prouvé qu'il en possède exactement ![]() et
qu'on a donc fini, mais son
condisciple plus observateur remarquera que nous ne savons pas encore si dans
l'énumération
et
qu'on a donc fini, mais son
condisciple plus observateur remarquera que nous ne savons pas encore si dans
l'énumération
![]() figurent bien
figurent bien ![]() éléments
distincts.
éléments
distincts.
Prouvons donc ce dernier fait ; supposons que dans cette
énumération il y ait
deux termes ![]() et
et ![]() qui représentent le même
élément du groupe, avec
pourtant
qui représentent le même
élément du groupe, avec
pourtant ![]() . On aurait alors
. On aurait alors ![]() . Mais par ailleurs, comme
. Mais par ailleurs, comme ![]() , on
obtient
, on
obtient ![]() et donc
et donc
![]() , et comme
, et comme
![]() et
et ![]() , on obtient
, on obtient
![]() . Mais ceci contredit la définition de
. Mais ceci contredit la définition de ![]() comme le plus petit
entier supérieur ou égal à
comme le plus petit
entier supérieur ou égal à ![]() tel que
tel que ![]() .
L'hypothèse était donc
absurde, et l'énumération décrivant
.
L'hypothèse était donc
absurde, et l'énumération décrivant
![]() à l'étape 1 est une
énumération sans répétition.
à l'étape 1 est une
énumération sans répétition.
Le nombre d'éléments de
![]() est donc bien égal à
est donc bien égal à ![]() , et
l'étape 1 est prouvée.
, et
l'étape 1 est prouvée.
Étape intermédiaire 3 : si l'ordre de ![]() est infini,
le théorème est vrai.
est infini,
le théorème est vrai.
Preuve de l'étape 3. Dans ce cas, tout le travail consiste à
prouver que
![]() est un ensemble infini.
La vérification est du
même esprit qu'à l'étape 2, en plus simple : on va
prouver que pour
est un ensemble infini.
La vérification est du
même esprit qu'à l'étape 2, en plus simple : on va
prouver que pour ![]() , les
éléments
, les
éléments ![]() et
et ![]() de
de
![]() sont distincts. Pour ce faire,
supposons que deux d'entre eux soient égaux ; on
aurait alors
sont distincts. Pour ce faire,
supposons que deux d'entre eux soient égaux ; on
aurait alors ![]() , avec
pourtant
, avec
pourtant
![]() et
et ![]() ne serait pas d'ordre infini. Ainsi
l'étape 3 est prouvée.
ne serait pas d'ordre infini. Ainsi
l'étape 3 est prouvée.![]()
Démonstration : Laissée au lecteur, en lui rappelant l'existence
dans ce cours d'un théorème dit «de Lagrange» et en lui
conseillant tout de même de bien distinguer entre ordre (cardinal)
et ordre (d'un élément), comme déjà mentionné.![]()
Histoire d'utiliser encore un peu la notion d'ordre, donnons un énoncé qui peut servir pour gagner du temps dans tel ou tel exercice très concret.
1. L'ensemble ![]() n'est pas vide.
n'est pas vide.
2. Pour tous ![]() de
de ![]() , le produit
, le produit ![]() est aussi dans
est aussi dans ![]() .
.
En d'autres termes, dans le cas particulier d'un sous-ensemble d'un groupe fini (et seulement dans ce cas !) on peut faire des économies et éviter de travailler sur les ennuyeux symétriques pour examiner un potentiel sous-groupe.
Pour enfoncer le clou sur la nécessité de
l'hypothèse selon laquelle ![]() est fini, on pensera au cas
est fini, on pensera au cas
![]() et
et
![]() .
.
Démonstration : La seule difficulté est évidemment de vérifier la propriété (iii)
de la définition des «sous-groupes». Prenons donc un élément
![]() de
de ![]() . On commence par traiter à part le cas stupide où
. On commence par traiter à part le cas stupide où
![]() , et où il est clair qu'on a aussi
, et où il est clair qu'on a aussi
![]() .
Pour le cas sérieux où
.
Pour le cas sérieux où ![]() , considérons le sous-groupe
, considérons le sous-groupe
![]() de
de ![]() . Ce sous-groupe est fini,
puisqu'inclus dans
. Ce sous-groupe est fini,
puisqu'inclus dans ![]() . On déduit donc du théorème
précédent (en fait de sa partie la plus facile,
l'étape 3 de sa preuve) que
. On déduit donc du théorème
précédent (en fait de sa partie la plus facile,
l'étape 3 de sa preuve) que ![]() est d'ordre fini. Notons
est d'ordre fini. Notons
![]() l'ordre de
l'ordre de ![]() ; comme
; comme ![]() , on a l'inégalité
, on a l'inégalité
![]() et donc
et donc
![]() ; écrivons l'identité
; écrivons l'identité
![]() ,
et revenons dans cette formule à la définition de
,
et revenons dans cette formule à la définition de
![]() : on obtient
: on obtient
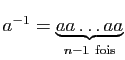 comme produit d'un nombre
positif d'exemplaires de
comme produit d'un nombre
positif d'exemplaires de ![]() ; par la propriété
2 de l'énoncé de la proposition, on en déduit que
; par la propriété
2 de l'énoncé de la proposition, on en déduit que
![]() .
.![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales