- Représenter graphiquement dans
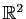 le graphe de la relation
le graphe de la relation
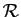 .
.
- Est-ce une relation d'ordre ? une relation d'équivalence ?

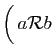 et
et 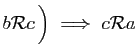
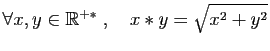
![$\displaystyle \forall x,y\in\mathbb{R}\;,\quad x\ast y=\sqrt[3]{x^3+y^3}
$](img456.gif)
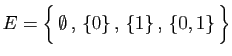
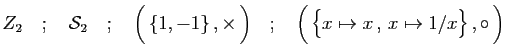
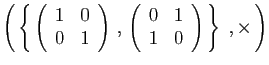
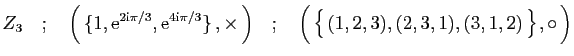
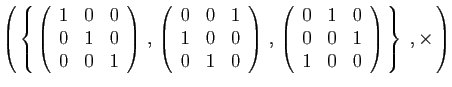
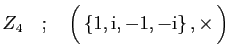
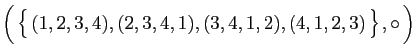
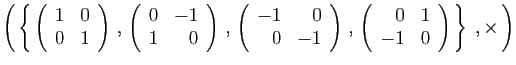
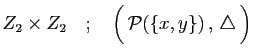
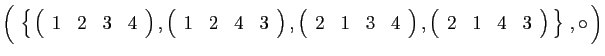
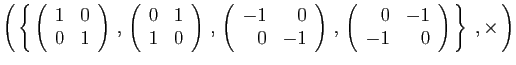
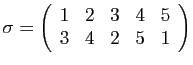 et
et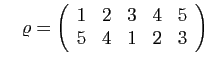
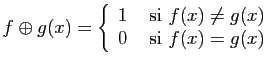
Montrer que ![]() est un isomorphisme de
est un isomorphisme de ![]() vers
vers ![]() , pour les lois
, pour les lois
![]() et
et ![]() . En déduire que
. En déduire que
![]() est un groupe
abélien, dans lequel chaque élément est son propre symétrique.
est un groupe
abélien, dans lequel chaque élément est son propre symétrique.
Dans toute la suite, ![]() désigne
un groupe dans lequel chaque élément est son propre
symétrique.
désigne
un groupe dans lequel chaque élément est son propre
symétrique.
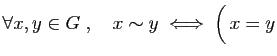 ou
ou 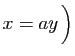
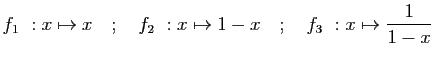
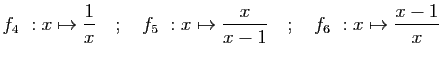
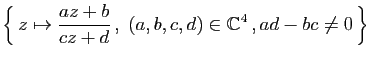
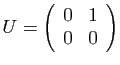 et
et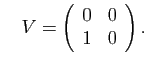
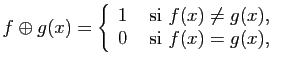 et
et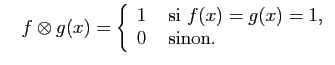
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales