Supposons que l'on utilise un nombre ![]() comme unité pour mesurer les multiples d'un autre :
comme unité pour mesurer les multiples d'un autre :
![]() . Pour tout
. Pour tout ![]() , on trouve un nombre entier
d'unités,
, on trouve un nombre entier
d'unités,
![]() , puis un reste qui est inférieur
à
, puis un reste qui est inférieur
à ![]() . Si
. Si ![]() est rationnel, il n'y a qu'un nombre fini de restes
possibles. Par contre si
est rationnel, il n'y a qu'un nombre fini de restes
possibles. Par contre si
![]() , non seulement il y a une
infinité de restes possibles, mais ces restes sont denses dans
l'intervalle
, non seulement il y a une
infinité de restes possibles, mais ces restes sont denses dans
l'intervalle ![]() . Nous commençons par le cas particulier
. Nous commençons par le cas particulier ![]() .
.
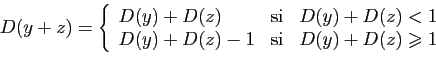
Fixons
![]() . Il existe
. Il existe ![]() tel que
tel que
![]() . Mais aussi, il existe
. Mais aussi, il existe ![]() tel que
tel que
![]() , donc
, donc
![]() . Posons
. Posons
![]() et
et
![]() . Toujours parce
que
. Toujours parce
que ![]() est irrationnel,
est irrationnel, ![]() ne peut pas être entier.
Ecrivons :
ne peut pas être entier.
Ecrivons :
Soient ![]() et
et ![]() deux réels tels que
deux réels tels que ![]() , et
, et
![]() . Soit
. Soit
![]() un entier tel que
un entier tel que
![]() . Soit
. Soit ![]() le plus petit
entier tel que
le plus petit
entier tel que
![]() . On a
. On a
![]() , ce qui montre
que l'ensemble
, ce qui montre
que l'ensemble ![]() est dense dans
est dense dans ![]() .
. ![]()
Considérons maintenant deux réels ![]() et
et ![]() incommensurables. Si
incommensurables. Si ![]() est un
réel, on notera
est un
réel, on notera ![]() («
(«
![]() modulo
modulo ![]() »),
le réel
»),
le réel ![]() , qui
appartient à l'intervalle
, qui
appartient à l'intervalle ![]() . Si
. Si ![]() et
et ![]() sont incommensurables, alors l'ensemble
sont incommensurables, alors l'ensemble
![]() est dense dans
est dense dans ![]() . Ceci découle
de la proposition 6 appliquée à
. Ceci découle
de la proposition 6 appliquée à ![]() .
.
Par exemple, puisque ![]() est irrationnel,
est irrationnel, ![]() et
et ![]() le
sont aussi. Donc
le
sont aussi. Donc ![]() et
et ![]() sont incommensurables. D'après ce qui
précède,
sont incommensurables. D'après ce qui
précède,
![]() est dense dans
est dense dans
![]() . On déduit de la continuité des fonctions
. On déduit de la continuité des fonctions ![]() et
et
![]() que
que
![]() et
et
![]() sont denses dans
sont denses dans ![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales