Exercice 2
Soient  ,
, 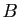 et
et 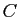 trois assertions. Démontrer que les
équivalences suivantes sont toujours vraies, d'abord à l'aide des
tables de vérité, ensuite en utilisant les opérations entre
connecteurs logiques. Traduire chacune des assertions en langage
courant, en remplaçant
trois assertions. Démontrer que les
équivalences suivantes sont toujours vraies, d'abord à l'aide des
tables de vérité, ensuite en utilisant les opérations entre
connecteurs logiques. Traduire chacune des assertions en langage
courant, en remplaçant  par «je mange»,
par «je mange», 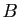 par «je bois»
et
par «je bois»
et 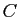 par «je fume».
par «je fume».
-
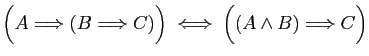 .
.
-
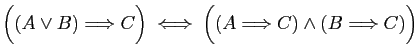 .
.
-
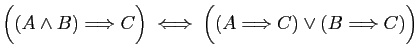 .
.
-
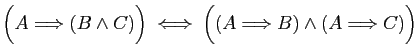 .
.
-
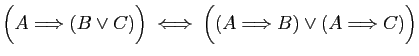 .
.
Exercice 3
On introduit un nouveau connecteur logique, dit barre de Scheffer, noté 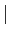 , dont la table de vérité est la suivante :
, dont la table de vérité est la suivante :
- Donner une expression de
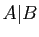 en utilisant les connecteurs usuels :
en utilisant les connecteurs usuels : 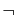 ,
, 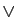 ,
, 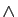 .
.
- Montrer que tous les connecteurs peuvent être remplacés par ce seul connecteur, en exprimant
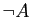 ,
, 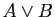 ,
, 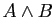 et
et
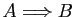 en utilisant seulement la barre de Scheffer et, si nécessaire, des parenthèses.
en utilisant seulement la barre de Scheffer et, si nécessaire, des parenthèses.
Exercice 4
On considère les quatre assertions suivantes :

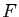 : je fume,
: je fume,

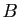 : je bois,
: je bois,

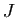 : je mange du jambon,
: je mange du jambon,

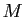 : j'ai des moustaches.
: j'ai des moustaches.
Exprimer sous forme symbolique les phrases suivantes :
- Je fume et je bois, mais je n'ai pas de moustache.
- Quand je fume, je ne bois pas.
- Chaque fois que je mange du jambon, je ne fume pas mais je bois.
- Si je mange du jambon ou si je bois, alors je ne fume pas.
- Il suffit que j'aie des moustaches pour que je mange du jambon.
- Il faut que je mange du jambon et que je boive pour que je fume.
- Une condition nécessaire pour que je boive et que je fume est que je
mange du jambon.
- Je fume et je bois, si et seulement si je mange du jambon ou j'ai des
moustaches.
- De deux choses l'une : soit je bois et je mange du jambon, soit si
j'ai une moustache alors je ne fume pas.
En supposant que les valeurs de vérité respectives de 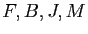 sont
sont
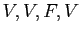 , trouver les valeurs de vérité des phrases
précédentes.
, trouver les valeurs de vérité des phrases
précédentes.
Exercice 5
Exprimer sous forme symbolique les raisonnements suivants et
vérifier qu'ils sont corrects.
- Si je vais à Londres, j'irai aussi à Oxford. Soit je vais à
Londres, soit je dépense mon argent à autre chose. Si je vais à
Oxford, je verrai John. Si je dépense mon argent à autre chose, je
verrai John. Donc je verrai John.
- Si j'ai de l'argent ou si je bois du vin alors je chante en me rasant et je
suis content. Donc je n'ai pas d'argent ou bien je chante en
me rasant.
- Soit je mange, soit je bois, et si je mange je ne fume pas. Comme je
ne bois pas, je ne fume pas.
- Si Pierre est marié, alors Jean est marié, et si Jean est marié,
alors Louis l'est aussi. De plus, soit Jean est célibataire, soit il
est marié et Louis est célibataire. Donc Pierre est célibataire.
- Si on ne danse pas, je m'asseois. Si je m'asseois, je bois et je
fume. Si on danse je m'amuse. Or je m'ennuie. Donc je fume.
- Si je ne m'asseois pas, je bois. Si je bois, on danse et de plus je
fume. Si je m'asseois, je m'amuse. Or je m'ennuie. Donc je fume.
- Si je marche, je sue. Si je ne me fatigue pas, je ne sue pas. Or je ne
me fatigue pas. Donc je ne marche pas.
- Si
 dit la vérité,
dit la vérité, 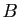 ment. Si
ment. Si 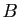 ment,
ment, 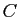 ment. Si
ment. Si 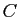 ment,
ment, 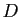 dit la vérité.
dit la vérité. 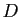 ment ou bien
ment ou bien 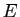 ment.
ment.  ne ment
pas. Donc
ne ment
pas. Donc 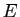 ment.
ment.
Exercice 6
Trois commerçants habitent dans 3 maisons situées aux numéros
21, 23 et 25 de la même rue. Le boucher habite dans la maison
jaune, qui est à côté de la rouge mais qui n'est pas à
côté de la verte. L'épicier, qui n'est pas suisse, habite à
côté du Français. L'Italien habite au numéro 21 et sa
maison n'est pas jaune. Quelle est la nationalité du pharmacien,
quelle est la couleur de sa maison, et où habite-t-il ?
Exercice 7
Trois personnes, un policier un berger et un assassin,
habitent dans 3 maisons situées aux numéros
19, 21 et 23 de la même rue. Le policier habite au numéro 23 et
sa maison n'est pas rouge. La maison rouge est à côté de la
maison bleue mais pas à côté de la maison jaune. L'Italien
habite dans la maison rouge. Le Français, qui n'est pas berger,
habite à côté de l'assassin. Quelle est la couleur de la maison
de l'assassin et où habite-t-il ?
Exercice 10
Soient  ,
, 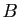 et
et 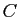 trois sous-ensembles d'un ensemble
trois sous-ensembles d'un ensemble 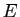 .
Ecrire en fonction de
.
Ecrire en fonction de 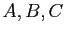 les ensembles
correspondant aux assertions suivantes.
les ensembles
correspondant aux assertions suivantes.
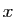 appartient aux trois.
appartient aux trois.
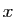 appartient au moins à l'un d'entre eux.
appartient au moins à l'un d'entre eux.
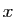 appartient à deux d'entre eux au plus.
appartient à deux d'entre eux au plus.
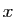 appartient à l'un d'entre eux exactement.
appartient à l'un d'entre eux exactement.
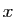 appartient à deux d'entre eux au moins.
appartient à deux d'entre eux au moins.
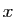 appartient à l'un d'entre eux au plus.
appartient à l'un d'entre eux au plus.
Exercice 11
Soit 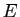 un ensemble. Soient
un ensemble. Soient  et
et 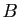 deux sous-ensembles de
deux sous-ensembles de 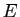 . On
appelle :
. On
appelle :

- différence de
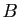 dans
dans  et on note
et on note
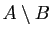 l'ensemble
l'ensemble
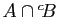 ,
,

- différence symétrique de
 et
et 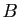 et on note
et on note 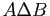 l'ensemble
l'ensemble
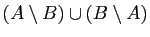 .
.
- Ecrire sous forme logique les propriétés «
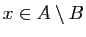 »
et «
»
et «
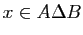 » à l'aide des propriétés «
» à l'aide des propriétés «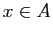 » et
«
» et
«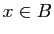 ». Démontrer les égalités ensemblistes suivantes.
». Démontrer les égalités ensemblistes suivantes.
-
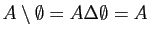 .
.
-
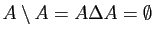 .
.
-
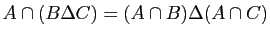 .
.
-
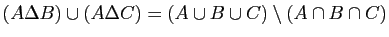 .
.
- Donner une représentation sous forme de diagramme de Venn de tous
les ensembles définis dans cet exercice.
Exercice 12
Soient  ,
, 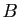 et
et 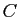 trois sous-ensembles d'un ensemble
trois sous-ensembles d'un ensemble 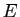 .
.
- Simplifier l'expression
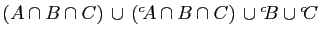 .
.
- Démontrer que
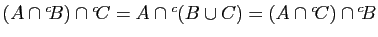 .
.
- Démontrer que
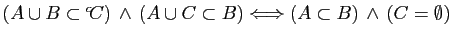 .
.
Exercice 13 (D'après Lewis Caroll)
. Parmi les combattants d'une grande bataille,
au moins 70% ont perdu un 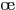 il, au moins 75% une oreille, au
moins 80% un bras, et au moins 85% une jambe. Quelle est la
proportion minimale des combattants qui ont perdu les 4 ?
il, au moins 75% une oreille, au
moins 80% un bras, et au moins 85% une jambe. Quelle est la
proportion minimale des combattants qui ont perdu les 4 ?
Exercice 14
Un centre de langue propose des cours d'Albanais, de Bantou et de
Chinois. Sur 93 élèves, 54 étudient l'Albanais, 51 le
Bantou ou le Chinois, 27 le Chinois mais pas le Bantou, 3 ni
l'Albanais ni le Chinois, et 12 étudient les 3 langues.
- Combien d'élèves étudient à la fois le Bantou et le Chinois ?
- Combien d'élèves étudient l'Albanais ou le Bantou mais pas
le Chinois ?
- Combien d'élèves n'étudient ni le Bantou ni le Chinois ?
- Combien d'élèves étudient une seule langue ?
- Combien d'élèves étudient exactement deux langues ?
Exercice 15
Pour chacune des assertions suivantes :

-
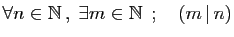 ,
,

-
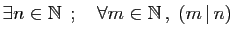 ,
,

-
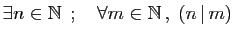 ,
,

-
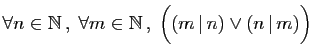 ,
,

-
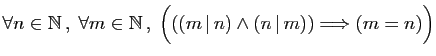 ,
,

-
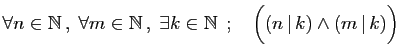 .
.
- Lire à haute voix et comprendre.
- Dire si l'assertion est vraie ou fausse et le démontrer.
- Ecrire la négation, lire à haute voix et comprendre.
Exercice 16
On note
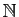 l'ensemble des entiers naturels,
l'ensemble des entiers naturels,  l'ensemble
des nombres pairs, et
l'ensemble
des nombres pairs, et 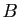 l'ensemble des nombres premiers.
Exprimer sous forme symbolique les phrases suivantes.
l'ensemble des nombres premiers.
Exprimer sous forme symbolique les phrases suivantes.
- Tout nombre pair est divisible par 2.
- Aucun nombre impair n'est divisible par 2.
- Il n'existe pas de nombre premier pair distinct de 2.
- Tout nombre premier distinct de 2 est impair.
- Il existe un nombre pair qui divise tout nombre pair.
- Tout nombre premier divise au moins un nombre pair
Exercice 17
On note
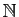 l'ensemble des entiers naturels,
l'ensemble des entiers naturels,  l'ensemble
des nombres pairs, et
l'ensemble
des nombres pairs, et 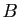 l'ensemble des nombres premiers.
Ecrire en langage courant et comprendre
la signification des expressions logiques suivantes.
l'ensemble des nombres premiers.
Ecrire en langage courant et comprendre
la signification des expressions logiques suivantes.
-
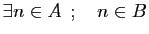 .
.
-
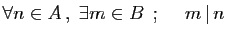 .
.
-
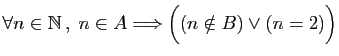 .
.
-
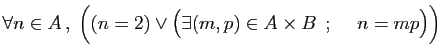 .
.
-
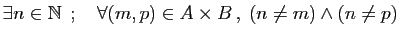 .
.
-
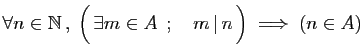 .
.
-
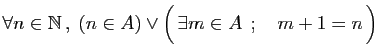 .
.
Exercice 18
Représenter sur un diagramme de Venn les ensembles suivants.

- Ensemble
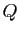 des quadrilatères.
des quadrilatères.

- Ensemble
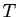 des trapèzes.
des trapèzes.

- Ensemble
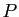 des parallélogrammes.
des parallélogrammes.

- Ensemble
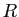 des rectangles.
des rectangles.

- Ensemble
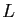 des losanges.
des losanges.

- Ensemble
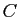 des carrés.
des carrés.
Exprimer sous forme logique, puis ensembliste, les phrases
suivantes.
- Tout carré est un rectangle.
- Tout rectangle qui est aussi un losange est un carré.
- Il existe des parallélogrammes qui ne sont pas des rectangles.
- Si un losange est un rectangle alors c'est un carré.
- Une condition nécessaire pour qu'un trapèze soit un carré est
que ce soit un rectangle.
- Pour qu'un trapèze soit un rectangle
il suffit que ce soit un carré.
- Il existe des quadrilatères qui ne sont ni des
rectangles, ni des losanges.
- Il existe des parallélogrammes qui ne sont ni des rectangles, ni des
losanges.
Exercice 19
Si 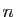 est un entier, on note «
est un entier, on note «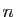 modulo 5» le reste de la division
euclidienne de
modulo 5» le reste de la division
euclidienne de 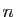 par
par 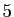 .
Les applications suivantes sont définies sur
.
Les applications suivantes sont définies sur
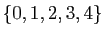 , à
valeurs dans lui-même.
Représentez-les sur un diagramme. Sont-elles injectives ?
surjectives ? bijectives ? Représentez le diagramme de
, à
valeurs dans lui-même.
Représentez-les sur un diagramme. Sont-elles injectives ?
surjectives ? bijectives ? Représentez le diagramme de 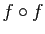 .
.
-
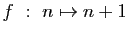 modulo
modulo 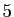 .
.
-
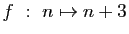 modulo
modulo 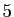 .
.
-
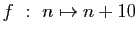 modulo
modulo 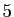 .
.
-
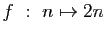 modulo
modulo 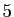 .
.
-
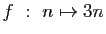 modulo
modulo 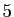 .
.
-
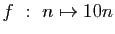 modulo
modulo 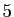 .
.
Exercice 20
Si 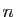 est un entier, on note «
est un entier, on note «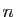 modulo 6» le reste de la division
euclidienne de
modulo 6» le reste de la division
euclidienne de 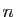 par
par 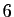 .
Les applications
.
Les applications 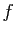 suivantes sont définies sur
suivantes sont définies sur
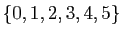 ,
à valeurs dans lui-même.
Représentez-les sur un diagramme. Sont-elles injectives ?
surjectives ? bijectives ? Représentez le diagramme de
,
à valeurs dans lui-même.
Représentez-les sur un diagramme. Sont-elles injectives ?
surjectives ? bijectives ? Représentez le diagramme de 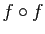 .
.
-
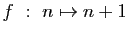 modulo
modulo 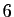 .
.
-
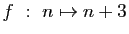 modulo
modulo 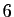 .
.
-
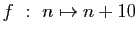 modulo
modulo 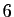 .
.
-
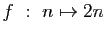 modulo
modulo 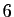 .
.
-
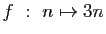 modulo
modulo 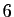 .
.
-
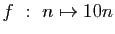 modulo
modulo 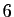 .
.
Exercice 21
On considère les applications suivantes, de
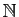 vers
vers
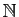 .
Sont-elles injectives ?
surjectives ? bijectives ?
.
Sont-elles injectives ?
surjectives ? bijectives ?
-
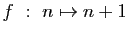 .
.
-
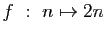 .
.
-
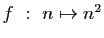 .
.
-
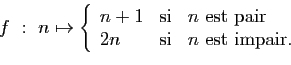
-
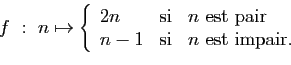
-
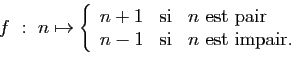
-
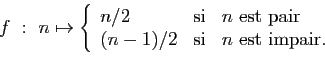
Exercice 22
On considère les applications suivantes, de
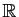 vers
vers
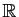 .
Sont-elles injectives ?
surjectives ? bijectives ?
.
Sont-elles injectives ?
surjectives ? bijectives ?
-
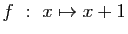 .
.
-
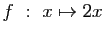 .
.
-
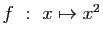 .
.
-
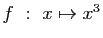 .
.
-
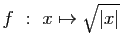 .
.
-
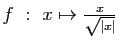 si
si 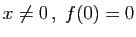 .
.
-
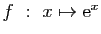 .
.
-
 .
.
Exercice 25
Les applications suivantes sont-elles injectives ? surjectives ?
bijectives ?
-
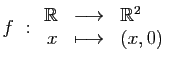
-
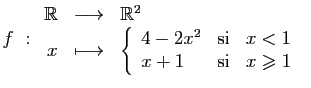
-
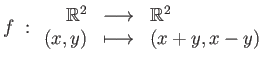
Exercice 27
Soit 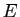 un ensemble et
un ensemble et  un sous-ensemble de
un sous-ensemble de 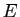 . On appelle «fonction
indicatrice de
. On appelle «fonction
indicatrice de  » et on note
» et on note
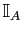 l'application de
l'application de 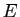 vers
vers 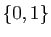 qui à
qui à 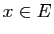 associe
associe 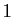 si
si 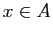 , 0 si
, 0 si
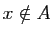 . Soient
. Soient  et
et 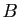 deux sous-ensembles de
deux sous-ensembles de 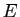 . Démontrer
les assertions suivantes.
. Démontrer
les assertions suivantes.
-
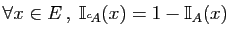 .
.
-
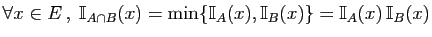 .
.
-
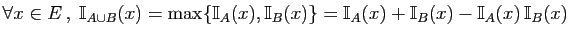 .
.
Exercice 28
Soient 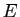 et
et 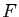 deux ensembles,
deux ensembles, 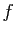 une application de
une application de 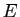 vers
vers
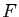 . Soient
. Soient  et
et 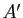 deux sous-ensembles de
deux sous-ensembles de 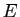 . Soient
. Soient
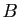 et
et 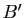 deux sous-ensembles de
deux sous-ensembles de 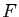 .
Démontrer les assertions suivantes.
.
Démontrer les assertions suivantes.
-
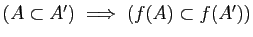 .
.
-
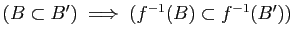 .
.
-
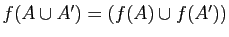 .
.
-
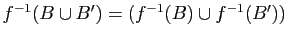 .
.
-
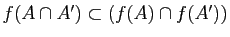 .
.
-
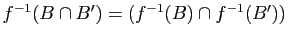 .
.
-
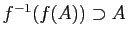 .
.
-
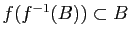 .
.
-
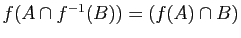 .
.
-
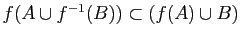 .
.
Exercice 29
Ecrire chacune des assertions suivantes comme une
implication.
Ecrire et démontrer sa contraposée.
- Aucun nombre impair n'est la somme de deux nombres impairs.
- Tout nombre premier strictement supérieur à 2 est impair.
- Soient
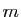 et
et 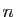 deux entiers impairs tels que
deux entiers impairs tels que
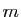 divise
divise 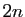 . Alors
. Alors 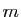 divise
divise 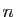 .
.
- Soient
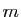 et
et 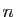 deux entiers tels que
deux entiers tels que 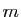 divise
divise 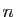 . Alors
. Alors 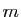 et
et
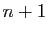 sont premiers entre eux (ils n'ont aucun diviseur commun autre
que
sont premiers entre eux (ils n'ont aucun diviseur commun autre
que 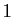 ).
).
- Si le produit de deux entiers strictement supérieurs à 1
est le carré d'un entier alors chacun des deux est le carré
d'un entier ou bien ils ont un diviseur commun autre que
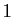 .
.
Exercice 30
Démontrer par récurrence les assertions suivantes.
-
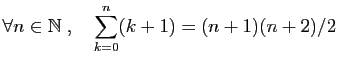 .
.
-
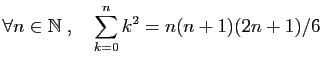 .
.
-
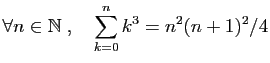 .
.
-
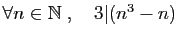 .
.
-
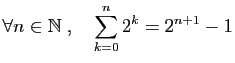 .
.
-
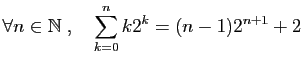 .
.
-
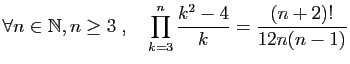 .
.
-
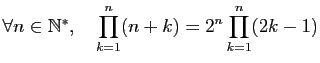 .
.
Exercice 31
Soient 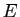 un ensemble fini non vide et
un ensemble fini non vide et 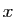 un élément fixé de
un élément fixé de
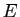 . On considère les relations
. On considère les relations 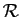 définies par les assertions
suivantes.
définies par les assertions
suivantes.

-
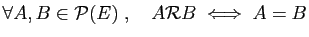 .
.

-
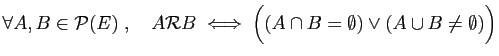 .
.

-
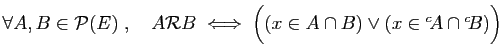 .
.
Pour chacune de ces relations.
- Montrer que
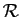 est une relation d'équivalence sur
est une relation d'équivalence sur
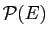 .
.
- Décrire l'ensemble quotient
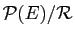 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
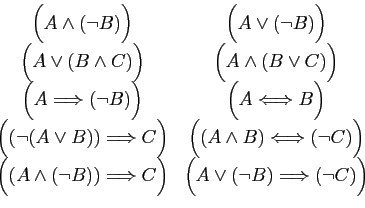
 par «je mange»,
par «je mange», 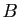 par «je bois»
et
par «je bois»
et 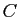 par «je fume».
par «je fume».
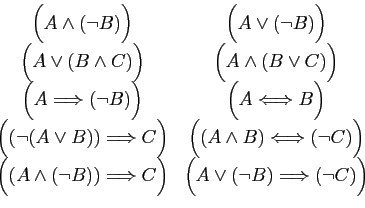
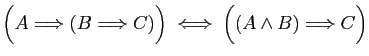 .
.
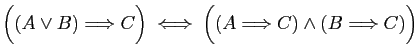 .
.
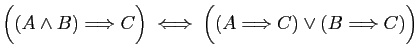 .
.
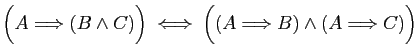 .
.
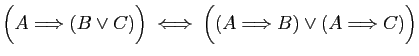 .
.

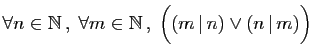 ,
,
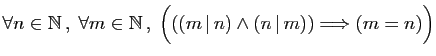 ,
,
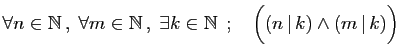 .
.
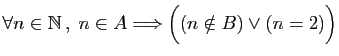 .
.
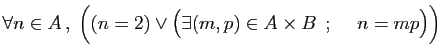 .
.
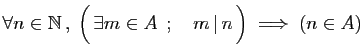 .
.
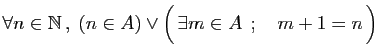 .
.
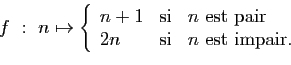
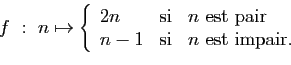
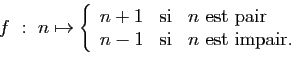
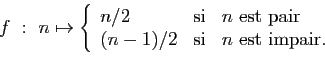
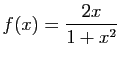 .
.
![$\displaystyle g : \begin{cases}[ -1, 1]\to[-1, 1]&\\
x\to f (x)\end{cases}$](img550.gif)
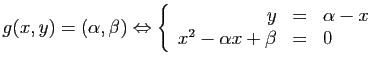
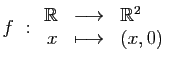
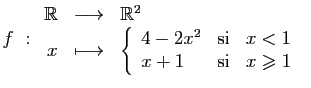
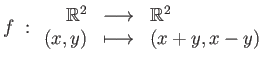
![]() est bijective. Dans l'un quelconque des
cas ci-dessus, montrer que
est bijective. Dans l'un quelconque des
cas ci-dessus, montrer que ![]() est bijective et calculer son inverse.
est bijective et calculer son inverse.
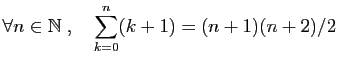 .
.
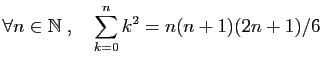 .
.
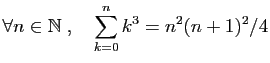 .
.
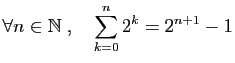 .
.
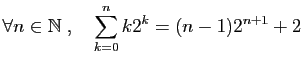 .
.
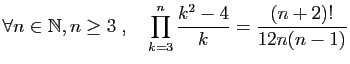 .
.
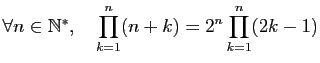 .
.
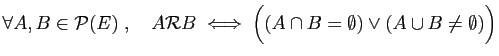 .
.
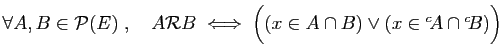 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales