Définition 6
Soit 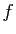 une fonction définie sur un intervalle
une fonction définie sur un intervalle 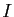 ouvert non vide
de
ouvert non vide
de
 . On dit que
. On dit que 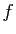 est continue sur
est continue sur 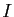 si
si 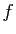 est
continue en tout point de
est
continue en tout point de 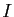 .
.
Cette définition comporte une petite ambiguïté pour les
intervalles qui ne sont pas ouverts. Nous conviendrons qu'une fonction
continue sur ![$ [a,b]$](img295.gif) est continue en tout point de
est continue en tout point de ![$ ]a,b[$](img156.gif) et que de
plus, elle est
continue à droite en
et que de
plus, elle est
continue à droite en 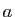 et à gauche en
et à gauche en 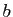 .
.
Le résultat important de cette section est le théorème des
valeurs intermédiaires.
La figure 3 illustre le théorème des valeurs
intermédiaires. Le résultat est tout à fait intuitif : si une
fonction continue prend deux valeurs distinctes sur un intervalle,
elle prend nécessairement toutes les valeurs entre ces deux-là :
le graphe d'une fonction continue n'a pas de saut vertical.
Figure 3:
Théorème des valeurs intermédiaires.
|
|
Démonstration : Par définition de la borne inférieure, et de la borne
supérieure, il existe
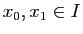 tels que
tels que
Quitte à remplacer 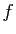 par
par 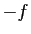 , nous pouvons supposer sans perte de
généralité que
, nous pouvons supposer sans perte de
généralité que 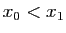 .
Soit
.
Soit 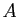 l'ensemble des
l'ensemble des
![$ x\in [x_0,x_1]$](img307.gif) tels que
tels que
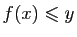 . L'ensemble
. L'ensemble 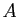 est non vide (il contient
est non vide (il contient 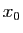 ), et
majoré par
), et
majoré par 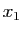 . Donc il admet une borne supérieure finie. Soit
. Donc il admet une borne supérieure finie. Soit
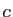 cette borne supérieure.
cette borne supérieure.
Nous allons démontrer que
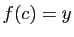 , en utilisant la continuité de
, en utilisant la continuité de 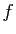 .
Soit
.
Soit
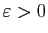 . Puisque
. Puisque 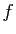 est continue en
est continue en 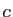 , il existe
, il existe 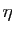 tel
que
tel
que
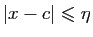 implique
implique
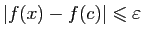 . Or par
définition de la borne supérieure, il existe
. Or par
définition de la borne supérieure, il existe 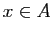 tel que
tel que
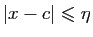 . Fixons un tel
. Fixons un tel 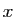 . Puisque
. Puisque
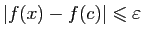 et
et
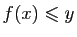 , alors nécessairement
, alors nécessairement
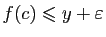 .
.
Par définition de la borne supérieure,
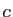 est le plus petit des majorants de
est le plus petit des majorants de  . Fixons maintenant
. Fixons maintenant
 tel que
tel que
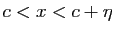 . Alors
. Alors 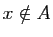 , donc
, donc
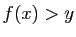 , et
, et
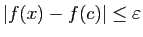 . On en déduit que
. On en déduit que
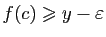 .
.
Nous avons donc démontré que pour tout
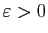 ,
,
ce qui entraîne 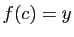 .
. Les deux résultats suivants sont des formulations équivalentes du
théorème des valeurs intermédiaires.
Les deux résultats suivants sont des formulations équivalentes du
théorème des valeurs intermédiaires.
Corollaire 2
- Si une fonction continue sur un intervalle prend des valeurs positives
et des valeurs négatives, alors elle s'annule sur cet intervalle.
- L'image par une application continue d'un intervalle est un intervalle.
Il est naturel de se demander si l'image par une application continue
d'un intervalle est un intervalle du même type (infini, ouvert...
). Le seul résultat général concerne les intervalles fermés
bornés.
Démonstration : elle utilise le théorème de
Bolzano-Weierstrass, qui affirme que
de toute suite 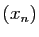 , à valeurs
dans l'intervalle
, à valeurs
dans l'intervalle ![$ [a,b]$](img295.gif) , on peut extraire une sous-suite
convergente. Nous traitons la borne supérieure
, on peut extraire une sous-suite
convergente. Nous traitons la borne supérieure 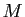 , la
démonstration est analogue pour
, la
démonstration est analogue pour 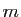 . Supposons
. Supposons 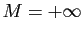 . Pour
tout
. Pour
tout 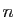 , il existe
, il existe
![$ x_n\in [a,b]$](img332.gif) tel que
tel que 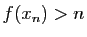 . Donc la suite
. Donc la suite
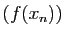 tend vers
tend vers 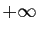 . De la suite
. De la suite
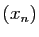 , on peut extraire une sous-suite convergente. Soit
, on peut extraire une sous-suite convergente. Soit 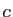 la
limite de cette sous-suite. Par la continuité de
la
limite de cette sous-suite. Par la continuité de 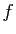 , les images des
termes de la sous-suite convergent vers
, les images des
termes de la sous-suite convergent vers 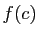 , ce qui contredit le
fait que
, ce qui contredit le
fait que 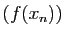 tend vers
tend vers 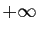 . Donc
. Donc 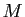 est finie.
est finie.
Puisque la borne supérieure est finie, pour tout
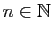 , il
existe
, il
existe
![$ x_n\in [a,b]$](img332.gif) tel que
tel que
Donc la suite 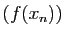 converge vers
converge vers 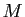 .
De la suite
.
De la suite 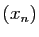 , on peut extraire une sous-suite, convergeant
vers
, on peut extraire une sous-suite, convergeant
vers
![$ c\in [a,b]$](img336.gif) . En utilisant à nouveau la continuité, on en
déduit que
. En utilisant à nouveau la continuité, on en
déduit que 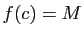 .
. En général les bornes
En général les bornes 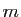 et
et 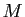 sont différentes des valeurs de
sont différentes des valeurs de
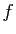 en
en 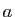 et
et 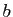 . Le cas des fonctions monotones est
particulier. Vous avez sans doute déjà rencontré le résultat
qui suit sous le nom de théorème de la bijection.
. Le cas des fonctions monotones est
particulier. Vous avez sans doute déjà rencontré le résultat
qui suit sous le nom de théorème de la bijection.
Théorème 13
Soit 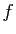 une fonction continue, strictement monotone sur un intervalle
une fonction continue, strictement monotone sur un intervalle
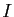 .
.
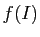 est un intervalle, dont les bornes sont les limites de
est un intervalle, dont les bornes sont les limites de 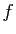 aux
bornes de
aux
bornes de 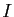
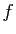 est une bijection de
est une bijection de 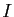 vers
vers 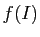
- la bijection réciproque
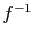 est continue sur
est continue sur 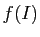 et
strictement monotone, de même sens que
et
strictement monotone, de même sens que 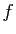 .
.
Démonstration : Quitte à remplacer 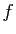 par
par 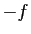 , nous pouvons supposer sans perte de
généralité que
, nous pouvons supposer sans perte de
généralité que 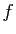 est strictement croissante. Ceci entraîne
que
est strictement croissante. Ceci entraîne
que 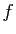 est injective. Supposons que
est injective. Supposons que 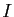 soit l'intervalle ouvert
soit l'intervalle ouvert ![$ ]a,b[$](img156.gif) ,
, 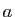 et
et 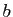 étant éventuellement
infinis. La démonstration s'adapte sans problème au cas où
l'intervalle est fermé d'un côté ou des deux.
étant éventuellement
infinis. La démonstration s'adapte sans problème au cas où
l'intervalle est fermé d'un côté ou des deux.
Observons que pour tout
![$ x_0\in ]a,b[$](img339.gif)
Posons
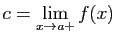
et
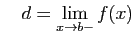
Soit
![$ y\in ]c,d[$](img343.gif) . D'après le théorème des valeurs
intermédiaires, il existe
. D'après le théorème des valeurs
intermédiaires, il existe
![$ x\in ]a,b[$](img344.gif) tel que
tel que 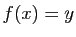 .
Donc
.
Donc
![$ f(]a,b[)=]c,d[$](img346.gif) , et comme
, et comme 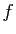 est injective, c'est une bijection
de
est injective, c'est une bijection
de ![$ ]a,b[$](img156.gif) vers
vers ![$ ]c,d[$](img347.gif) . Pour tout
. Pour tout
![$ x_1,x_2\in ]a,b[$](img348.gif) ,
,
Donc la bijection réciproque 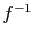 est
elle-aussi strictement croissante. Il reste à démontrer qu'elle
est continue. Soit
est
elle-aussi strictement croissante. Il reste à démontrer qu'elle
est continue. Soit
![$ y_0\in ]c,d[$](img350.gif) et
et
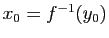 . Soit
. Soit
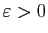 tel
que
tel
que
Posons
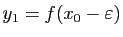 et
et
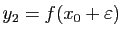 . Alors
. Alors
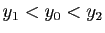 . Soit
. Soit
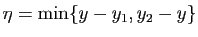 . Pour tout
. Pour tout 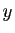 tel que
tel que
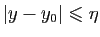 ,
on a
,
on a
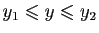 , donc
, donc
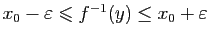 . D'où le résultat.
. D'où le résultat.  Si
Si 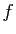 est bijective, à tout couple
est bijective, à tout couple 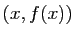 du graphe de
du graphe de 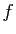 ,
correspond le couple
,
correspond le couple 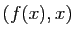 du graphe de
du graphe de 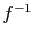 : les deux
graphes se déduisent l'un de l'autre par la transformation
: les deux
graphes se déduisent l'un de l'autre par la transformation
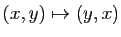 , qui est la symétrie par rapport à la
première bissectrice (figure 4).
, qui est la symétrie par rapport à la
première bissectrice (figure 4).
Figure 4:
Graphe d'une bijection monotone et de sa réciproque.
|
|
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() est le plus petit des majorants de
est le plus petit des majorants de ![]() . Fixons maintenant
. Fixons maintenant
![]() tel que
tel que
![]() . Alors
. Alors ![]() , donc
, donc
![]() , et
, et
![]() . On en déduit que
. On en déduit que
![]() .
.
![]() ,
,
![]() , il
existe
, il
existe
![]() tel que
tel que
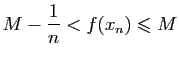
![]()
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales