Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
- Soit
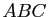 un triangle non aplati d'un plan affine
un triangle non aplati d'un plan affine 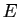 et
et 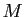 le point de coordonnées barycentriques
le point de coordonnées barycentriques 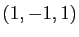 dans le repère affine
dans le repère affine 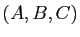 de
de 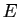 . Montrer que le quadrilatère
. Montrer que le quadrilatère 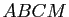 est un parallélogramme.
est un parallélogramme.
- Soit
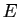 un espace affine de dimension
un espace affine de dimension 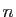 rapporté à un repère cartésien
rapporté à un repère cartésien
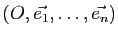 . Donner l'équation de la direction d'un hyperplan affine d'équation
. Donner l'équation de la direction d'un hyperplan affine d'équation
 . Donner une condition nécessaire et suffisante pour que deux hyperplans affines d'équations respectives
. Donner une condition nécessaire et suffisante pour que deux hyperplans affines d'équations respectives
 et
et
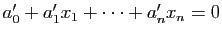 soient parallèles.
soient parallèles.
- Donner deux caractérisations de l'enveloppe convexe d'une partie non vide d'un espace affine.
- Donner la nature géométrique de la composée de deux homothéties.
- Montrer qu'une application affine
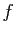 d'un espace affine
d'un espace affine 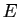 dans lui-même dont la partie linéaire est
dans lui-même dont la partie linéaire est
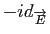 est une symétrie centrale.
est une symétrie centrale.
Exercice 1 :
Dans l'espace affine 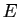 de dimension
de dimension 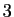 rapporté à un repère cartésien
rapporté à un repère cartésien
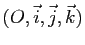 , soit
, soit 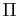 le plan d'équation
le plan d'équation
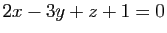 et
et 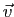 le vecteur de composantes
le vecteur de composantes 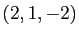 . On note
. On note 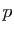 la projection sur
la projection sur 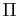 dans la direction du vecteur
dans la direction du vecteur 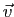 et
et 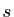 la symétrie par rapport au plan
la symétrie par rapport au plan 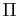 dans la direction de
dans la direction de 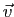 .
.
- Écrire les coordonnées
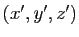 du point
du point 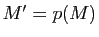 en fonction des coordonnées
en fonction des coordonnées 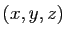 du point
du point 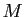 .
.
- En déduire la matrice
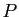 dans la base
dans la base
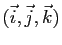 de la partie linéaire
de la partie linéaire 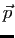 de
de 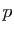 .
.
- Calculer la matrice
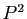 . Quel est le rang de
. Quel est le rang de 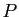 ?
?
- Écrire les coordonnées
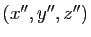 du point
du point 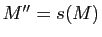 en fonction des coordonnées
en fonction des coordonnées 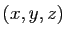 du point
du point 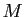 .
.
- En déduire la matrice
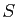 dans la base
dans la base
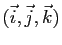 de la partie linéaire
de la partie linéaire 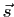 de
de 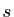 . Calculer
. Calculer 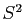 .
.
- Soit
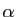 un réel. On rappelle que l'affinité
un réel. On rappelle que l'affinité 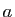 de base
de base 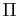 , de direction la droite vectorielle
, de direction la droite vectorielle
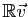 engendrée par
engendrée par 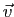 et de rapport
et de rapport 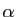 est l'application de
est l'application de 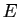 dans
dans 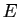 définie par
définie par
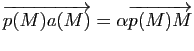 pour tout point
pour tout point 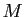 de
de 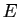 . Écrire, pour tout couple
. Écrire, pour tout couple 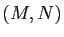 de points de
de points de 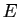 , le vecteur
, le vecteur
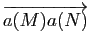 en fonction des vecteurs
en fonction des vecteurs
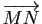 et
et
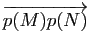 .
.
- En déduire que
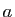 est affine et exprimer sa partie linéaire
est affine et exprimer sa partie linéaire 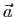 en fonction de
en fonction de 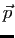 et de
et de
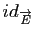 . Exprimer la matrice
. Exprimer la matrice 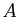 de
de 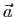 en fonction de la matrice
en fonction de la matrice 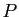 et de la matrice identité.
et de la matrice identité.
- Déterminer un polynôme du second degré annulant
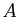 .
.
Exercice 2 :
Le but de l'exercice est d'étudier l'application 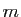 qui à un
qui à un 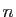 -uplet
-uplet
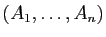 de points d'un espace affine
de points d'un espace affine 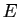 associe le
associe le 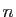 -uplet
-uplet
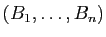 , où
, où 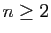 est un entier fixé et, pour
est un entier fixé et, pour
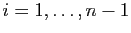 ,
, 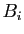 est le milieu du segment
est le milieu du segment
![$ [A_iA_{i+1}]$](img943.gif) et
et 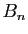 est le milieu du segment
est le milieu du segment ![$ [A_nA_1]$](img945.gif) . On note, pour tout point
. On note, pour tout point 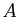 de
de 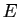 ,
, 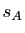 la symétrie centrale de centre
la symétrie centrale de centre 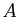 .
.
- Montrer que la composée
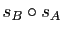 de deux symétries centrales est une translation dont on exprimera le vecteur en fonction de
de deux symétries centrales est une translation dont on exprimera le vecteur en fonction de 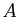 et
et 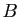 . En déduire que la composée d'un nombre pair de symétries centrales est une translation.
. En déduire que la composée d'un nombre pair de symétries centrales est une translation.
- Montrer que la composée d'un nombre impair de symétries centrales est une symétrie centrale.
- Soit
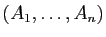 un
un 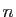 -uplet de points de
-uplet de points de 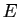 et
et
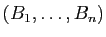 les points définis précédemment. On définit, pour
les points définis précédemment. On définit, pour
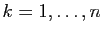 , des applications
, des applications 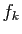 de
de 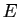 dans
dans 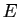 par
par
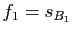 et
et
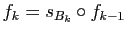 pour
pour 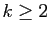 . Déterminer
. Déterminer 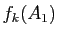 pour
pour
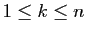 .
.
- On suppose
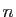 impair.
impair.
- a)
- Montrer que
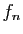 est une symétrie centrale dont on précisera le centre. En déduire que l'application
est une symétrie centrale dont on précisera le centre. En déduire que l'application 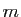 est une bijection de l'ensemble des
est une bijection de l'ensemble des 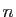 -uplets de points de
-uplets de points de 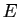 sur lui-même.
sur lui-même.
- b)
- Donner une construction des points
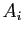 connaissant les points
connaissant les points 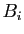 .
.
- On suppose
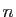 pair.
pair.
- a)
- Montrer que
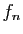 est une translation dont on écrira le vecteur en fonction des points
est une translation dont on écrira le vecteur en fonction des points
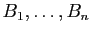 . En déduire une relation vérifiée par ces points.
. En déduire une relation vérifiée par ces points.
- b)
- Déterminer l'image de l'application
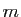 . Cette application est-elle injective ?
. Cette application est-elle injective ?
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
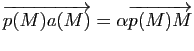 pour tout point
pour tout point 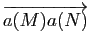 en fonction des vecteurs
en fonction des vecteurs
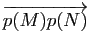 .
.
![]() qui à un
qui à un ![]() -uplet
-uplet
![]() de points d'un espace affine
de points d'un espace affine ![]() associe le
associe le ![]() -uplet
-uplet
![]() , où
, où ![]() est un entier fixé et, pour
est un entier fixé et, pour
![]() ,
, ![]() est le milieu du segment
est le milieu du segment
![]() et
et ![]() est le milieu du segment
est le milieu du segment ![]() . On note, pour tout point
. On note, pour tout point ![]() de
de ![]() ,
, ![]() la symétrie centrale de centre
la symétrie centrale de centre ![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales