-
 L'application
L'application 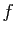 est continûment différentiable sur
est continûment différentiable sur
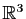 .
.
 La différentielle de
La différentielle de 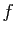 est une application linéaire de
est une application linéaire de
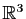 dans
dans
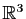 .
.
 Le gradient de
Le gradient de 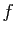 est une application linéaire de
est une application linéaire de
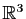 dans
dans
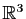 .
.
-
 Le gradient de
Le gradient de 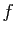 au point
au point
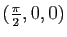 est nul.
est nul.
-
 Le gradient de
Le gradient de 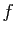 au point
au point
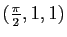 est nul.
est nul.
 La matrice jacobienne de
La matrice jacobienne de 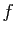 au point
au point 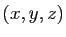 est une matrice
réelle
est une matrice
réelle 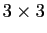 .
.
-
 La matrice hessienne de
La matrice hessienne de 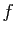 au point
au point 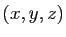 est une matrice
réelle
est une matrice
réelle 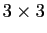 .
.
-
 La matrice hessienne de
La matrice hessienne de 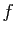 au point
au point 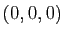 est la matrice nulle.
est la matrice nulle.
 La matrice hessienne de
La matrice hessienne de 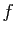 au point
au point
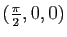 est la
matrice nulle.
est la
matrice nulle.
 La matrice hessienne de
La matrice hessienne de 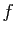 au point
au point
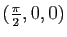 a toutes
ses valeurs propres strictement négatives.
a toutes
ses valeurs propres strictement négatives.
-
 La matrice hessienne de
La matrice hessienne de 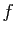 au point
au point
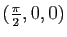 a pour
valeurs propres 0,
a pour
valeurs propres 0,
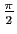 et
et
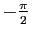 .
.
 Le point
Le point
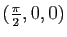 est un maximum local de
est un maximum local de 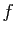 .
.
-
 La matrice hessienne de
La matrice hessienne de 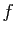 au point
au point
 a tous ses
coefficients strictement négatifs.
a tous ses
coefficients strictement négatifs.
-
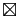 La matrice hessienne de
La matrice hessienne de 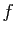 au point
au point
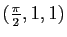 a pour
valeurs propres 0 et
a pour
valeurs propres 0 et
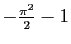 .
.
-
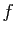 atteint son maximum au point
atteint son maximum au point
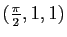 .
.
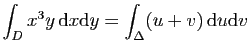
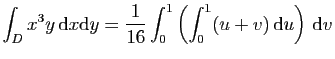
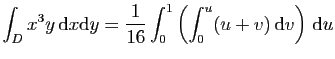
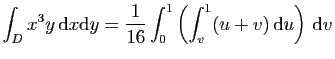
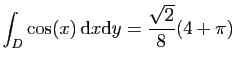
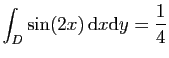
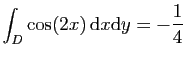
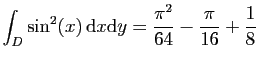
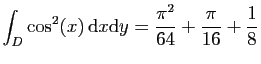
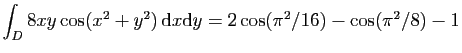
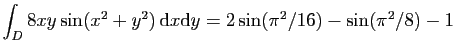
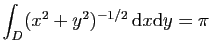
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales