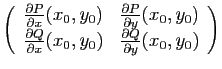
L'identification naturelle ![]() de
de
![]() et
et
![]() définie par
définie par
![]() est un isomorphisme de
est un isomorphisme de
![]() -espace vectoriel,
de plus
-espace vectoriel,
de plus
![]() .
.
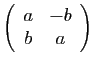
Supposons maintenant que, pour tout
![]() ,
,
![]() avec
avec
![]() ,
alors pour tout
,
alors pour tout
![]()
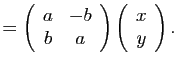 |
Finalement supposons que
![]() est une similitude de matrice
est une similitude de matrice
Fonctions holomorphes
Comme pour les fonctions d'une variable réelle on a les propriétes suivantes :
2) Soient ![]() une fonction définie au voisinage de
une fonction définie au voisinage de ![]() et
et
![]() -dérivable en
-dérivable en ![]() et
et ![]() une fonction définie au voisinage de
une fonction définie au voisinage de
![]() et
et
![]() -dérivable en
-dérivable en ![]() , alors
, alors ![]() est
est
![]() -dérivable en
-dérivable en ![]() et sa dérivée en
et sa dérivée en ![]() vaut
vaut
![]() .
.
3) Si ![]() est
est
![]() -dérivable en
-dérivable en ![]() et si
et si
![]() ,
,
![]() est définie au voisinage de
est définie au voisinage de ![]() ,
,
![]() -dérivable en
-dérivable en
![]() et
et
![]() .
.
(i) la fonction ![]() est
est
![]() -dérivable en
-dérivable en ![]() ;
;
(ii) la fonction ![]() est
est
![]() -différentiable en
-différentiable en ![]() et elle satisfait l'équation de Cauchy-Riemann
et elle satisfait l'équation de Cauchy-Riemann
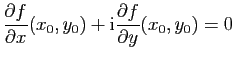
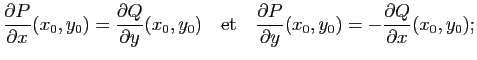
(iii) la fonction ![]() est
est
![]() -différentiable en
-différentiable en ![]() et sa différentielle et
et sa différentielle et
![]() -linéaire.
-linéaire.
En identifiant
![]() à
à
![]() on obtient
on obtient
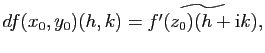
![]() D'après le Lemme 1,
l'application
D'après le Lemme 1,
l'application
![]() est
est
![]() -linéaire si et seulement si il
existe
-linéaire si et seulement si il
existe
![]() tels que sa matrice relativement à la base
canonique de
tels que sa matrice relativement à la base
canonique de
![]() est de la forme
est de la forme
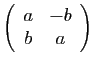
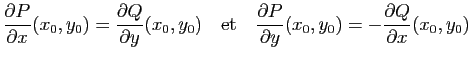
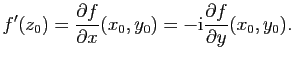
On note
![]() l'ensemble des fonctions holomorphes sur
l'ensemble des fonctions holomorphes sur ![]() .
.
Propriétés :
1) L'ensemble
![]() est une sous-algèbre de
est une sous-algèbre de
![]() ;
;
2) Si
![]() ne s'annule pas sur
ne s'annule pas sur ![]() ,
,
![]() ;
;
3) Si ![]() et
et ![]() sont deux ouverts de
sont deux ouverts de
![]() ,
,
![]() et
et
![]() deux fonctions holomorphes,
deux fonctions holomorphes, ![]() est holomorphe
sur
est holomorphe
sur ![]() .
.
Exemples :
1) L'application identique
![]() est
holomorphe sur
est
holomorphe sur
![]() ;
;
2) L'application
![]() n'est pas holomorphe sur
n'est pas holomorphe sur
![]() ;
;
3)L'application polynôme
![]() est holomorphe sur
est holomorphe sur
![]() ;
;
4) La fraction rationnelle
![]() , où
, où ![]() et
et ![]() sont
des polynômes, est holomorphe sur
sont
des polynômes, est holomorphe sur
![]() privé des zéros de
privé des zéros de ![]() ;
;
5) La somme d'une série entière définit une fonction holomorphe sur le disque ouvert de convergence de la série entière;
6) Les fonctions analytiques sur ![]() sont holomorphes sur
sont holomorphes sur ![]() (la
réciproque est vraie nous la montrerons dans la section
1.2).
(la
réciproque est vraie nous la montrerons dans la section
1.2).
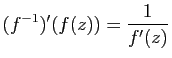 pour tout
pour tout
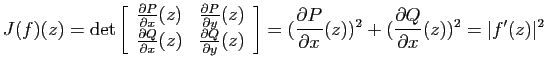
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales