Un espace vectoriel est un ensemble sur lequel sont définies :
- une addition interne (on peut ajouter entre eux deux éléments de
l'ensemble et cela donne un élément de l'ensemble)
- une multiplication externe (on peut multiplier un élément de
l'ensemble par un nombre réel et cela donne un élément de l'ensemble).
Ces deux opérations doivent vérifier certaines
propriétés de compatibilité
qui sont listées dans la définition 1.
Définition 1
On dit que 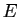 est un espace vectoriel sur
est un espace vectoriel sur
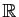 si
si 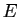 est muni d'une
addition et d'une multiplication externe vérifiant les
propriétés suivantes.
est muni d'une
addition et d'une multiplication externe vérifiant les
propriétés suivantes.
- Addition :
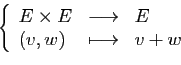
- Associativité :
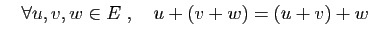
- Élément neutre :
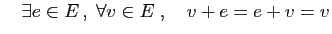
- Opposé :
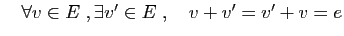
- Commutativité :
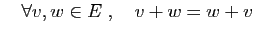
Ces propriétés font de 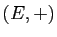 un groupe commutatif.
un groupe commutatif.
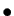
- Multiplication externe :
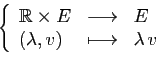
- 5.
- Associativité :
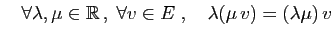
- 6.
- Élément neutre :
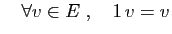
- 7.
- Distributivité (1) :
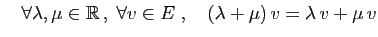
- 8.
- Distributivité (2) :
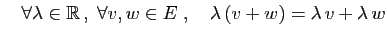
La proposition suivante nous autorisera à noter 0 l'élément
neutre pour l'addition (nous l'appellerons «vecteur nul»)
et 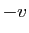 l'opposé de
l'opposé de 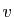 .
.
Proposition 1
Soit 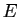 un espace vectoriel.
un espace vectoriel.
- Le produit par le réel 0 d'un vecteur
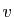 quelconque est
l'élément neutre pour l'addition :
quelconque est
l'élément neutre pour l'addition :
- Le produit par le réel
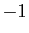 d'un vecteur
d'un vecteur 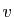 quelconque est
son opposé pour l'addition :
quelconque est
son opposé pour l'addition :
Démonstration : Notons (provisoirement) 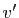 l'opposé de
l'opposé de 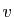 pour l'addition :
pour l'addition : 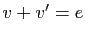 .
En utilisant les propriétés de la définition 1 :
.
En utilisant les propriétés de la définition 1 :
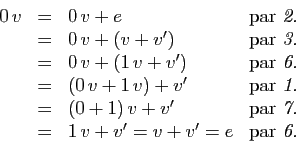
Ceci démontre le premier point. Pour le second, il suffit
d'écrire
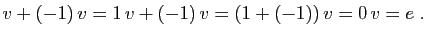
 Le singleton contenant seulement le vecteur nul est un espace
vectoriel particulier. Ce n'est pas le plus intéressant.
Voici quelques ensembles, naturellement munis d'une
addition et d'une multiplication externe. Nous démontrerons plus
loin que tous sont effectivement des espaces vectoriels.
Le singleton contenant seulement le vecteur nul est un espace
vectoriel particulier. Ce n'est pas le plus intéressant.
Voici quelques ensembles, naturellement munis d'une
addition et d'une multiplication externe. Nous démontrerons plus
loin que tous sont effectivement des espaces vectoriels.
- Nombres complexes :
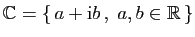 .
.
L'ensemble des complexes est muni de l'addition et
de la multiplication par un réel, qui agissent sur les parties
réelles et imaginaires.
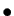
- Addition :
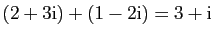
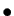
- Multiplication externe :
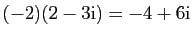
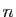 -uplets de réels :
-uplets de réels :
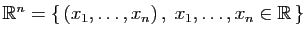 .
.
L'ensemble des 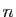 -uplets de réels (couples pour
-uplets de réels (couples pour 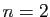 ,
triplets pour
,
triplets pour 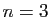 , ...) est muni de l'addition et
de la multiplication par un réel, coordonnée par coordonnée.
, ...) est muni de l'addition et
de la multiplication par un réel, coordonnée par coordonnée.
- Addition :
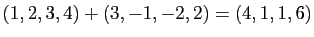
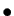
- Multiplication externe :
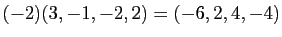
- Matrices à coefficients réels :
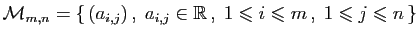 .
.
L'ensemble des matrices à 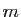 lignes et
lignes et 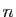 colonnes, à
coefficients réels, est muni de l'addition et
de la multiplication par un réel,
coefficient par coefficient.
colonnes, à
coefficients réels, est muni de l'addition et
de la multiplication par un réel,
coefficient par coefficient.
- Addition :
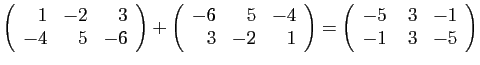
- Multiplication externe :
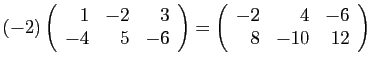
- Suites de réels :
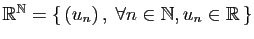 .
.
L'ensemble des suites de réels est
muni de l'addition et de la multiplication par un réel, terme à terme.
- Addition :
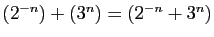
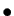
- Multiplication externe :
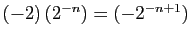
- Polynômes :
![$ \mathbb{R}[X]=\{a_0+a_1X+\ldots+a_n X^n ,\;n\in\mathbb{N},
(a_0,\ldots,a_n)\in\mathbb{R}^{n+1}\}$](img47.gif) .
.
L'ensemble des polynômes d'une variable, à coefficients réels
est aussi muni naturellement d'une addition et d'une
multiplication externe.
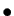
- Addition :
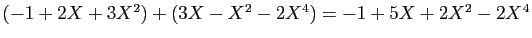
- Multiplication externe :
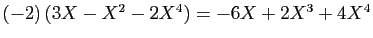
- Applications :
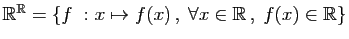 .
.
L'ensemble des applications de
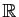 dans
dans
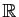 est
muni de l'addition des images et de leur multiplication par un réel.
est
muni de l'addition des images et de leur multiplication par un réel.
- Addition :
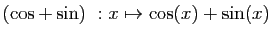
- Multiplication externe :
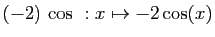
Il est inutile de s'inquiéter de la quantité de
propriétés à vérifier dans la définition
1. Dans tous les exemples que l'on rencontrera,
les opérations sont parfaitement naturelles et leurs propriétés
évidentes. On ne vérifie d'ailleurs jamais les
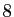 propriétés de la définition 1. La raison pour
laquelle c'est inutile sera explicitée dans la section
suivante. Remarquons seulement pour l'instant que tous
les exemples ci-dessus peuvent être mis en correspondance avec
l'ensemble des applications d'un certain ensemble
propriétés de la définition 1. La raison pour
laquelle c'est inutile sera explicitée dans la section
suivante. Remarquons seulement pour l'instant que tous
les exemples ci-dessus peuvent être mis en correspondance avec
l'ensemble des applications d'un certain ensemble 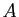 , dans
, dans
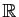 .
Cela va sans dire pour les
applications de
.
Cela va sans dire pour les
applications de
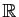 dans
dans
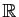 . Les
. Les 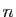 -uplets de réels sont
des applications de
-uplets de réels sont
des applications de
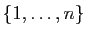 dans
dans
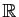 . Les
nombres complexes peuvent être identifiés à des couples de
réels, les matrices à des applications de
. Les
nombres complexes peuvent être identifiés à des couples de
réels, les matrices à des applications de
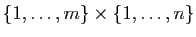 dans
dans
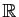 . Les
suites sont des applications de
. Les
suites sont des applications de
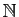 dans
dans
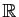 . Nous verrons plus
loin comment les polynômes se ramènent à des suites.
Nous nous contenterons donc de vérifier pour l'instant
que l'ensemble des applications
de
. Nous verrons plus
loin comment les polynômes se ramènent à des suites.
Nous nous contenterons donc de vérifier pour l'instant
que l'ensemble des applications
de 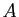 dans
dans
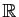 est un espace vectoriel.
est un espace vectoriel.
Démonstration : Chacune des propriétés requises par la définition 1
provient d'une propriété analogue des réels. Plutôt que de
répéter formellement les énoncés des propriétés, il est
plus intéressant de comprendre quels sont
les objets que l'on manipule. Par exemple, l'élément
neutre pour l'addition, même si on le note aussi
0 n'est pas le réel 0 : c'est l'application nulle.
De même, l'opposé de 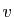 est l'application qui à
est l'application qui à 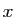 associe
associe
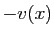 .
.
Considérons la propriété 5. de la définition
1.
Elle signifie ici :
«si on multiplie par 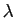 l'application qui à
l'application qui à
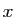 associe
associe
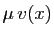 , on trouve la même chose que si on multiplie
par
, on trouve la même chose que si on multiplie
par
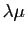 l'application qui à
l'application qui à 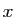 associe
associe 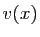 ,
c'est-à-dire l'application qui à
,
c'est-à-dire l'application qui à 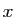 associe
associe
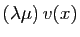 ,»
,»
...
ce qui est bien vrai, n'est-ce pas ?
Nous laissons au lecteur le plaisir de traduire de même chacune des
propriétés de la définition 1. Nous ne parlerons dans ce chapitre que d'espaces vectoriels sur
Nous ne parlerons dans ce chapitre que d'espaces vectoriels sur
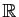 . Cependant, on peut remplacer
. Cependant, on peut remplacer
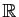 par un autre corps
commutatif dans la définition 1, sans modifier notablement la
théorie. Hormis
par un autre corps
commutatif dans la définition 1, sans modifier notablement la
théorie. Hormis
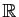 , les corps les plus utilisés sont
, les corps les plus utilisés sont
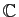 et
et
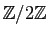 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
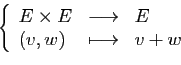
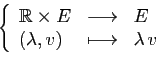
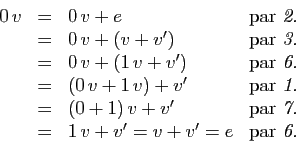
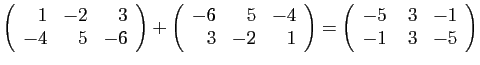
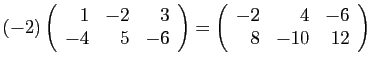
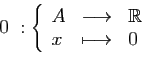
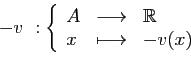
l'application qui à
associe
, on trouve la même chose que si on multiplie par
l'application qui à
associe
, c'est-à-dire l'application qui à
associe
,»
![]() Nous ne parlerons dans ce chapitre que d'espaces vectoriels sur
Nous ne parlerons dans ce chapitre que d'espaces vectoriels sur
![]() . Cependant, on peut remplacer
. Cependant, on peut remplacer
![]() par un autre corps
commutatif dans la définition 1, sans modifier notablement la
théorie. Hormis
par un autre corps
commutatif dans la définition 1, sans modifier notablement la
théorie. Hormis
![]() , les corps les plus utilisés sont
, les corps les plus utilisés sont
![]() et
et
![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales