Questions de cours :
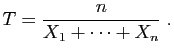
ic.moy qui prend en entrée un vecteur de
données X et un niveau de confiance nc
(valeur par défaut t.test).
ic.sym qui prend en entrée un vecteur de
données X et un niveau de confiance nc
(valeur par défaut nv pour l'échantillon X, basé sur la loi gamma.
test.gamma qui prend en entrée
un vecteur de données X et une valeur du paramètre
la0, et qui retourne les p-valeurs de 2 tests unilatéraux de
l'hypothèse
la0, contre
la0. Le premier test est
le test de la moyenne (fonction t.test), le second
utilise la loi de pgamma).
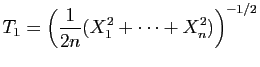 et
et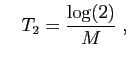
boxplot). Représenter la vraie valeur par un trait horizontal.
reg.est qui prend en entrée un vecteur
de données X, et retourne la valeur de compare.est, qui prend en entrée une
valeur lambda, deux entiers E et n. La fonction
tire E échantillons de taille n de la loi exponentielle de
paramètre lambda. Elle calcule pour chacun les estimations
obtenues par E estimations pour chacun des 5
estimateurs. Elle retourne dans une table ces 5 erreurs quadratiques
moyennes.
qqnorm),
shapiro.test),
ks.test).
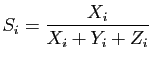 et
et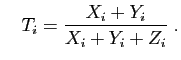
wilcox.test)
beta.
Dans l'échantillon chisq.test).
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales