 La fonction
La fonction 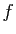 est dérivable sur un intervalle ouvert
contenant 0.
est dérivable sur un intervalle ouvert
contenant 0.
-
 La fonction
La fonction 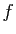 est continue en 0.
est continue en 0.
-
 La dérivée de
La dérivée de 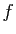 en 0 est égale à
en 0 est égale à 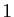 .
.
 Si
Si 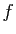 est
est 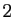 fois dérivable sur un intervalle ouvert contenant
0, alors
fois dérivable sur un intervalle ouvert contenant
0, alors
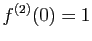 .
.
-
 Si
Si 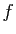 est
est 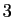 fois dérivable sur un intervalle ouvert contenant
0, alors
fois dérivable sur un intervalle ouvert contenant
0, alors
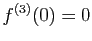 .
.
 La fonction
La fonction
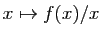 admet un développement limité
d'ordre
admet un développement limité
d'ordre 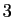 en 0.
en 0.
-
 La fonction
La fonction
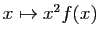 admet un développement limité
d'ordre
admet un développement limité
d'ordre 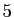 en 0.
en 0.

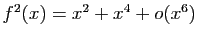 .
.
-
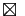
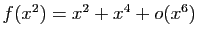 .
.

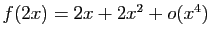 .
.

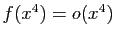 .
.
-
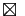
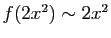 .
.
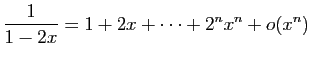
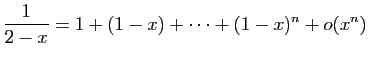
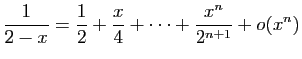
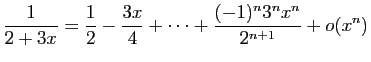
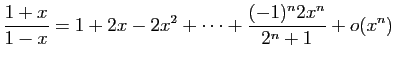
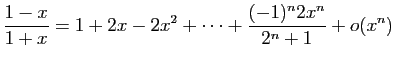
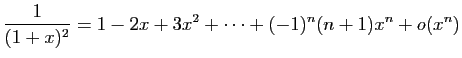
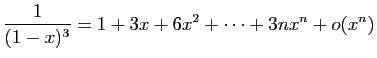
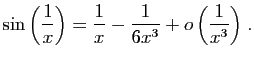
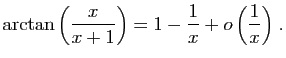
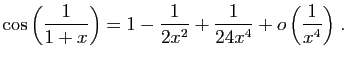
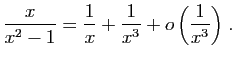
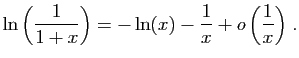
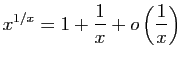
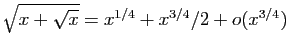
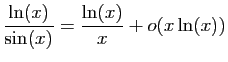
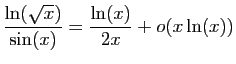
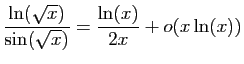
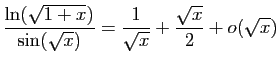
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales