Nous commençons par extraire des sections précédentes
les résultats les plus utiles pour le calcul pratique.
- (R1)
- Le déterminant d'une matrice triangulaire est le produit des
coefficients de la diagonale.
- (R2)
- On ne modifie pas un déterminant si on ajoute à une ligne (ou une
colonne) une combinaison linéaire des autres lignes (ou des autres
colonnes).
- (R3)
- Si on multiplie une ligne ou une colonne par une constante, le
déterminant est multiplié par cette même constante.
- (R4)
- On peut développer un déterminant selon ou une ligne ou une
colonne, grâce aux formules
où les 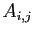 sont les cofacteurs.
sont les cofacteurs.
Attention, il faut appliquer ces résultats un par un et pas
simultanément ; en particulier, il convient d'éviter d'ajouter en
même temps des
combinaisons linéaires à plusieurs lignes ou colonnes, ce qui
engendre souvent des erreurs.
On ne se lance jamais dans le développement selon
ou une ligne ou une colonne, avant d'avoir utilisé les résultats
précédents, pour «faire apparaître des zéros».
La méthode algorithmique, sans astuce donc
conseillée, est la méthode du pivot de Gauss, qui procède par
transformations successives pour faire apparaître des zéros sous
la diagonale.
Une petite piqure de rappel sur un exemple n'est peut-être
pas superflue. Considérons la matrice
suivante.
Le coefficient d'indices 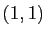 est non nul, il n'y a donc pas de
permutations à effectuer. Le premier pivot est
est non nul, il n'y a donc pas de
permutations à effectuer. Le premier pivot est 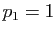 . Voici les
transformations qui annulent la première colonne au-dessous du pivot.
. Voici les
transformations qui annulent la première colonne au-dessous du pivot.
Le second pivot est 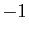 . Les transformations qui annulent le bas de la
seconde colonne sont les suivantes.
. Les transformations qui annulent le bas de la
seconde colonne sont les suivantes.
Pour obtenir un troisième pivot non nul, il faut échanger les deux
dernières colonnes.
Le troisième pivot est 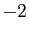 . Il ne reste qu'une ligne à transformer.
. Il ne reste qu'une ligne à transformer.
Constatez qu'à chaque étape de la méthode,
les transformations consistent à :
- ajouter à une ligne un multiple d'une autre, ce qui ne change
pas le déterminant ;
- permuter deux lignes ou deux colonnes, ce qui change le déterminant
en son opposé.
La matrice obtenue au bout du compte est triangulaire ; son
déterminant est le produit des coefficients diagonaux. Pour en déduire
le déterminant initial, il suffit de compter le nombre de
permutations de lignes ou de colonnes, et de changer le signe si ce
nombre est impair. Au bilan, le nombre d'opérations nécessaire au
calcul d'un déterminant d'ordre 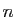 par la méthode du pivot de
Gauss est équivalent à
par la méthode du pivot de
Gauss est équivalent à
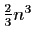 , ce qui est
incomparablement plus rapide que les
, ce qui est
incomparablement plus rapide que les 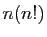 opérations de la
formule explicite.
Nous illustrons maintenant les méthodes de calcul sur quelques
exemples classiques.
opérations de la
formule explicite.
Nous illustrons maintenant les méthodes de calcul sur quelques
exemples classiques.
Proposition 12
Le déterminant
est :
Démonstration : La somme des éléments de chaque ligne vaut
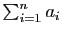 . On
commence donc par ajouter toutes les colonnes à la première, puis
on met
. On
commence donc par ajouter toutes les colonnes à la première, puis
on met
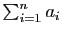 en facteur.
en facteur.
On conserve la première ligne, puis on retranche chaque ligne à la
suivante :
On développe alors suivant la première colonne :
Ce dernier déterminant est celui d'une matrice triangulaire : il est
le produit des éléments de la diagonale. 
Proposition 13
Le déterminant (dit «de Vandermonde»)
est :
Démonstration : Considérons le polynôme de degré 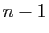 qui a pour racines
qui a pour racines
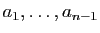 :
:
Ajoutons à la dernière colonne la première multipliée par
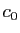 , la seconde multipliée par
, la seconde multipliée par 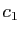 , etc. Par définition de
, etc. Par définition de
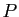 , ceci va annuler les éléments de la dernière colonne, sauf
le dernier :
, ceci va annuler les éléments de la dernière colonne, sauf
le dernier :
Si on développe suivant la dernière colonne,
Or
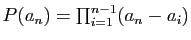 : d'où le résultat, par
récurrence.
Voici une autre démonstration. Le déterminant
: d'où le résultat, par
récurrence.
Voici une autre démonstration. Le déterminant
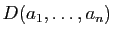 est un polynôme en
est un polynôme en
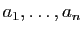 . Le développement selon une
ligne quelconque, montre que c'est un polynôme de degré
. Le développement selon une
ligne quelconque, montre que c'est un polynôme de degré 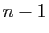 en
chacune des variables. Or il s'annule dès que deux d'entre elles
sont égales (puisqu'alors deux lignes coïncident). Donc
en
chacune des variables. Or il s'annule dès que deux d'entre elles
sont égales (puisqu'alors deux lignes coïncident). Donc
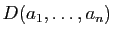 est un multiple du produit de
toutes les différences
est un multiple du produit de
toutes les différences 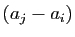 pour
pour
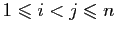 . Or ces deux polynômes sont de même degré en chacune
des variables.
Il ne reste donc qu'à déterminer la constante de proportionnalité. Pour
cela, examinons le terme en
. Or ces deux polynômes sont de même degré en chacune
des variables.
Il ne reste donc qu'à déterminer la constante de proportionnalité. Pour
cela, examinons le terme en 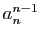 : il est égal au mineur
d'indices
: il est égal au mineur
d'indices 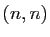 , qui est
, qui est
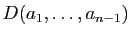 , affecté du signe
, affecté du signe
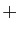 comme tous les mineurs diagonaux. Par récurrence, le coefficient
de proportionnalité cherché est donc
comme tous les mineurs diagonaux. Par récurrence, le coefficient
de proportionnalité cherché est donc 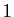 .
.
Proposition 14
Le déterminant (dit «circulant»)
est :
où 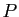 est le polynôme
est le polynôme
et les 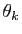 sont les racines
sont les racines 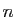 -ièmes de l'unité :
-ièmes de l'unité :
Démonstration : Notons 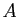 la matrice proposée. Soit
la matrice proposée. Soit 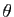 une racine
une racine 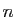 -ième
de l'unité (quelconque).
Considérons le vecteur (colonne)
-ième
de l'unité (quelconque).
Considérons le vecteur (colonne)
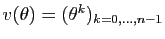 ,
et multiplions à droite la matrice
,
et multiplions à droite la matrice 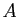 par
par 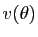 . La première
coordonnée du produit est
. La première
coordonnée du produit est
La seconde coordonnée est :
On vérifie de même, que pour
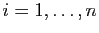 , la
, la
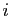 -ième coordonnée est
-ième coordonnée est
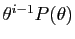 .
Donc
.
Donc
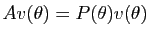 .
.
Considérons maintenant la famille de vecteurs
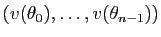 . Son déterminant est le
déterminant de Vandermonde de la proposition précédente : les
. Son déterminant est le
déterminant de Vandermonde de la proposition précédente : les
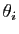 étant tous différents, il est non nul. Donc la famille
de vecteurs est une base. Notons-la
étant tous différents, il est non nul. Donc la famille
de vecteurs est une base. Notons-la 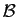 . Soit
. Soit 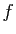 l'endomorphisme qui a pour matrice
l'endomorphisme qui a pour matrice 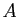 dans la base canonique. Sa
matrice dans la base
dans la base canonique. Sa
matrice dans la base 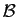 est la matrice diagonale dont les
coefficients diagonaux sont
est la matrice diagonale dont les
coefficients diagonaux sont
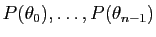 : son
déterminant est le produit
: son
déterminant est le produit
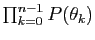 . Or
le déterminant de
. Or
le déterminant de 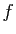 est le même quelle que soit la base
dans laquelle on écrit sa matrice. D'où le résultat.
est le même quelle que soit la base
dans laquelle on écrit sa matrice. D'où le résultat. 
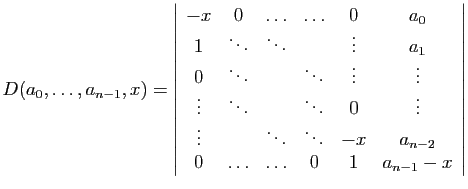
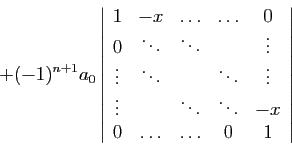
Proposition 15
Le déterminant
est :
La matrice pour 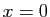 est la matrice
compagnon du polynôme ci-dessus : vous
comprendrez pourquoi quand vous étudierez la réduction des
endomorphismes.
Démonstration : Pour
est la matrice
compagnon du polynôme ci-dessus : vous
comprendrez pourquoi quand vous étudierez la réduction des
endomorphismes.
Démonstration : Pour 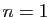 , la formule donne
, la formule donne
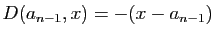 , elle est
donc correcte.
Développons suivant la première ligne :
, elle est
donc correcte.
Développons suivant la première ligne :
Si
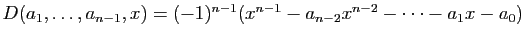 ,
alors l'expression ci-dessus donne bien
,
alors l'expression ci-dessus donne bien
d'où le résultat, par récurrence.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
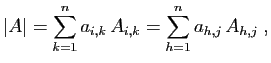
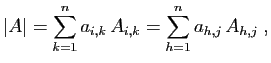
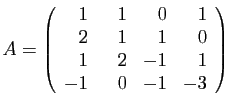
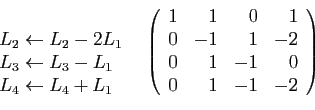
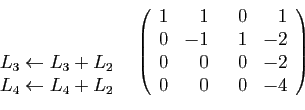
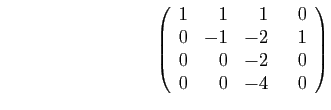
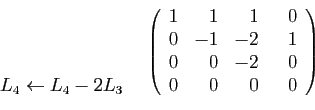
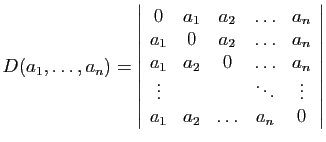
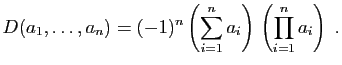
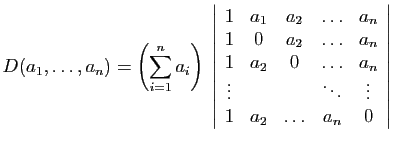
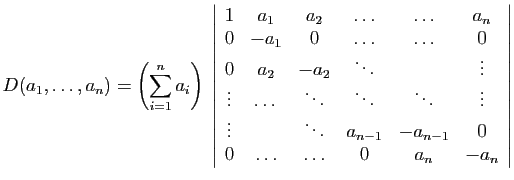
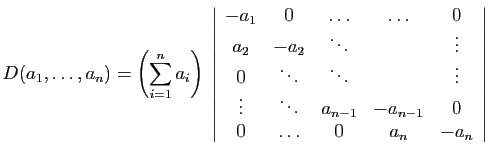
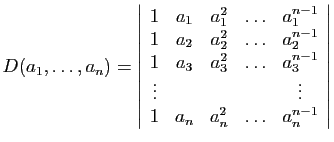
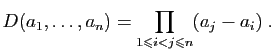
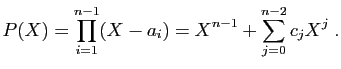
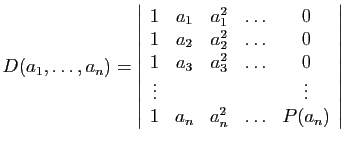
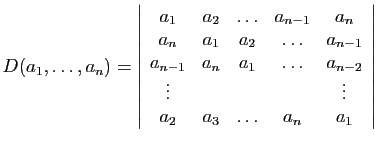
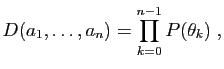
![]() . Son déterminant est le
déterminant de Vandermonde de la proposition précédente : les
. Son déterminant est le
déterminant de Vandermonde de la proposition précédente : les
![]() étant tous différents, il est non nul. Donc la famille
de vecteurs est une base. Notons-la
étant tous différents, il est non nul. Donc la famille
de vecteurs est une base. Notons-la ![]() . Soit
. Soit ![]() l'endomorphisme qui a pour matrice
l'endomorphisme qui a pour matrice ![]() dans la base canonique. Sa
matrice dans la base
dans la base canonique. Sa
matrice dans la base ![]() est la matrice diagonale dont les
coefficients diagonaux sont
est la matrice diagonale dont les
coefficients diagonaux sont
![]() : son
déterminant est le produit
: son
déterminant est le produit
![]() . Or
le déterminant de
. Or
le déterminant de ![]() est le même quelle que soit la base
dans laquelle on écrit sa matrice. D'où le résultat.
est le même quelle que soit la base
dans laquelle on écrit sa matrice. D'où le résultat. ![]()

 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales