Ce mémoire a été trouvé dans les papiers de M. Cellérier, professeur à Genève, mort l'année dernière.
Il est entièrement écrit de sa main sur un papier jauni par le temps ; l'auteur a mis sur la feuille qui le renfermait la suscription que voici : «Très important, et, je crois, nouveau. - rédaction correcte. Peut être publié tel quel.» Malheureusement, le Mémoire ne comporte aucune date, et il sera sans doute impossible de savoir si les résultats essentiels qu'il contient ont été, ou non, obtenus avant ceux que l'on doit à MM. Weierstrass, Schwarz, du Bois-Reymond, Darboux, Dini, etc. Quoi qu'il en soit, ils ont été obtenus indépendamment des travaux que nous venons de rappeler, comme le prouvera la lecture du Mémoire, et en particulier la phrase suivante que l'auteur n'aurait sûrement pas écrite s'il avait eu connaissance des recherches dont les fondements de l'Analyse ont été l'objet depuis une vingtaine d'années.Quelle phrase ?
On pourrait, par un raisonnement analogue, c'est-à-dire en partageanten intervalles de plus en plus petits, et considérant le nombre déterminé par la suite de leurs limites inférieures, démontrer quelques autres propriétés essentielles de toutes les fonctions continues, celles de ne pouvoir passer d'une valeur à une autre sans devenir exactement égale à tout nombre intermédiaire, d'être susceptible d'une valeur maxima et minima qu'elle atteint pour une valeur au moins de la variable, etc. Ces questions offrent peu d'intérêt, vu leur évidence. Nous remarquerons seulement que l'intégrale
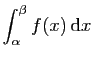
a un sens absolument déterminé, en désignant parEn clair, Cellérier avait parfaitement compris comment rendre rigoureux les énoncés portant sur une fonction continue définie sur un intervalle fermé borné : théorème des valeurs intermédiaires, extrema atteints... tout juste daigne-t-il préciser comment définir son intégrale. Mais ce n'était pas tout. Voici la définition de la continuité uniforme :la fonction. Si l'on partage l'intervalle
en
parties égales, puis chacune en
autres, et ainsi de suite à l'infini, on peut faire correspondre une somme de produits dont chacun est celui de la valeur commune de l'intervalle, par la valeur minima de la fonction quand la variable s'y trouve comprise ; la somme de ces produits correspondant à chaque intervalle étant désignée par
pour le premier mode de partage, par
pour le deuxième, et aisni de suite, ces nombres
formés suivant une loi déterminée, sont en nombre infini, constamment croissants, et la limite dont ils s'approchent est l'intégrale ci-dessus.
Une autre manière de concevoir la continuité consisterait à dire que, quelque petit que soitMais aussi la convergence uniforme des séries de fonctions :, on peut toujours trouver un nombre
tel qu'on ait
quand
,
et
étant compris entre
et
, du reste quelconques. Cela revient à dire qu'on peut trouver une limite
convenant à la fois à toutes les valeurs de
. Ce nouvel énoncé n'est point tout à fait équivalent au précédent.
Une série dont les termes sont fonctions continues entreCellérier donne la conséquence sur la continuité de la somme, puis sur son intégrale.,
sera aussi fonction continue entre ces deux limites si elle satisfait ce que nous nommerons la condition de convergence commune, c'est-à-dire si, quel que soit
, on peut trouver un nombre
qui convienne à la fois à toutes les valeurs de
.
Représentons toujours parIl n'en reste pas là.la somme d'une série convergente dont les termes sont fonctions continues de
quand cette variable croît de
à
. S'il y a une convergence commune, alors les intégrales des termes prises entre deux limites comprises entre
et
auront pour somme
prise entre les mêmes limites.
Considérons la fonction donnée par la série suivante.
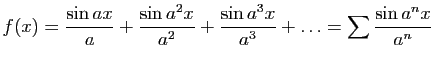
dans laquelleest un entier constant que nous supposerons positif et très grand. La série étant plus convergente que la progression
, il est clair qu'elle a une convergence commune entre deux valeurs quelconques de
, et que, par suite,
est une fonction continue.
Cette série nous fournira un exemple soit d'une fonction qui n'a jamais de dérivée, soit d'une fonction qui n'a jamais aucune période de croissance ou de décroissance ; ces propriétés seront plus aisées à vérifier en supposantLe premier exemple publié de fonction continue nulle part dérivable est celui de Weierstrass en 1875 ; On a su depuis que Bolzano en avait un avant. Cellérier a-t-il la priorité ? Il a laissé peu de traces dans l'histoire des mathématiques. Voici comment il figure dans les «souvenirs d'un arpenteur genevois»8.pair pour la première et impair pour la seconde.
Ce dernier, contemporain de mon père, n'écoutait jamais une leçon de mathématiques au collège. Interrogé, il levait le nez du livre qu'il lisait, s'informait de quoi il était question, improvisait une démonstration toujours satisfaisante et se replongeait dans sa lecture. J'ai eu de lui des leçons de calcul différentiel et intégral. Son extrême modestie lui a valu d'être dépouillé d'une gloire dont se para un mathématicien de Paris, professeur en Sorbonne. Ce professeur venait de déclarer en chaire qu'on ne savait pas intégrer les fonctions elliptiques. Raoul Pictet, qui se trouvait parmi les assistants, s'approcha de lui après la leçon et lui communiqua le procédé, qu'il tenait de Charles Cellérier, pour intégrer les équations différentielles elliptiques. La démonstration parut dans la nouvelle édition de son cours que le professeur français se hâta de faire paraître, mais le nom de Cellérier n'y figura pas.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales