Définition bifocale des coniques à centre

L'existence de deux couples foyer-directrice pour les coniques à centre permet d'en obtenir une autre caractérisation. Si on appelle en effet $F$ et $F'$ les foyers, $D$ et $D'$ les directrices correspondantes, $H$ et $H'$ les projetés d'un point $M$ de la conique sur $D$ et $D'$, on a les relations $MF=eMH$, $MF'=eMH'$.

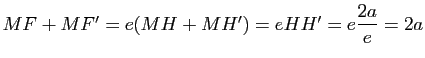Cas de l'ellipse L'ellipse est entièrement incluse dans la bande verticale délimitée par ses deux directrices ; il en résulte que tout point $M$ de l'ellipse appartient au segment $HH'$, d'où $MF+MF'=e(MH+MH')=eHH'=e\dfrac{2a}{e}=2a$. L'ellipse est donc incluse dans l'ensemble des points $M$ du plan vérifiant $MF+MF'=2a$.
Réciproquement, si un point $M$ du plan de coordonnées $(x,y)$ vérifie $MF+MF'=2a$, on déduit de la relation

$$(MF-MF')(MF+MF')=MF^2-MF'^2=[(x-c)^2+y^2]-[(x+c)^2+y^2]=-4cx$$

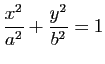que $MF-MF'=-2 e x$, puisque $e=c/a$, d'où $MF=a-ex$, et $MF^2=(x-c)^2+y^2=(a-ex)^2$, soit $x^2 (1-e^2)+y^2=b^2$ puisque $ea=c$ et $a^2-b^2=c^2$, ou encore, en divisant par $b^2$, $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$, ce qui montre que l'ensemble des points $M$ du plan vérifiant $MF+MF'=2a$ est inclus dans l'ellipse. L'ellipse est donc égale à cet ensemble.

Cas de l'hyperbole

L'hyperbole se compose au contraire de deux branches extérieures à la bande verticale délimitée par ses deux directrices. Il en résulte que pour tout point $M$ de l'hyperbole, on a $\vert MF-MF'\vert=e\vert MH-MH'\vert=2a$. L'une des branches de l'hyperbole est donc incluse dans l'ensemble des points $M$ du plan vérifiant $MF-MF'=2a$ et l'autre dans l'ensemble des points $M$ vérifiant $MF'-MF=2a$. Un calcul identique à celui opéré dans le cas de l'ellipse permet ici encore de vérifier que l'hyperbole est exactement l'ensemble des points $M$ du plan vérifiant $\vert MF-MF'\vert=2a$.

En résumé :

Proposition 3   Soient $F$ et $F'$ deux points distincts du plan et $c=FF'/2$ la demi-distance entre ces deux points.

1. Pour tout réel $a>c$, l'ensemble des points $M$ du plan vérifiant $MF+MF'=2a$ est l'ellipse de foyers $F$ et $F'$ et de grand axe $2a$.
2. Pour tout réel positif $a<c$, l'ensemble des points $M$ du plan vérifiant $\vert MF-MF'\vert=2a$ est l'hyperbole de foyers $F$ et $F'$ et de grand axe $2a$.

Le cercle peut apparaître ici encore comme un cas particulier d'ellipse pour laquelle les deux foyers seraient confondus.

Application : construction de l'ellipse par le procédé dit du jardinier.

Pour tracer une ellipse de foyers $F$ et $F'$ et de longueur de grand axe $2a>FF'$ donnés, il suffit de fixer deux piquets en $F$ et $F'$ et d'y attacher les extrémités d'une ficelle non élastique de longueur $2a$. Le trajet que l'on parcourt en tournant autour de $F$ et $F'$ tout en maintenant la ficelle tendue est l'ellipse cherchée.

Tableau 1: Coniques à centre

	Ellipse	Hyperbole
Équation réduite	$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$ $0<b<a$	$\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$
Représentation paramétrique	$x=a\cos t$ $y=b\sin t$ $0\leq t <2\pi$	$x=\varepsilon a\ch t$ $y=b\sh t$ $\varepsilon\in\{-1,+1\},\, t\in\mathbb{R}$
Distance focale	$FF'=2c$ $a^2=b^2+c^2$	$FF'=2c$ $c^2=a^2+b^2$
Excentricité	$e=\dfrac{c}{a}$	$e=\dfrac{c}{a}$
Longueur des axes	$AA'=2a$    grand axe $BB'=2b$    petit axe	$AA'=2a$    axe focal
Définition bifocale	$MF+MF'=2a$	$\vert\, MF-MF'\,\vert=2a$