Rang d'une matrice
Nous avons déjà défini la notion de rang pour une famille de
vecteurs et pour une application linéaire :
- le rang d'une famille de vecteurs est la dimension du sous espace
vectoriel qu'elle engendre,
- le rang d'une application linéaire est la dimension de son image.
Soient 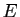 et
et 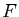 deux espaces vectoriels, et
deux espaces vectoriels, et 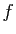 une application
linéaire de
une application
linéaire de 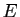 dans
dans 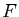 . Si
. Si
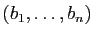 est une base de
est une base de
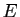 , l'image de
, l'image de 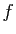 est le sous-espace vectoriel de
est le sous-espace vectoriel de 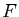 engendré par
engendré par
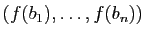 . Donc le rang de
. Donc le rang de 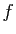 est aussi le rang de
la famille
est aussi le rang de
la famille
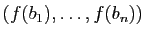 et ce, quelle que soit la base
et ce, quelle que soit la base
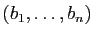 . Ce rang ne dépend pas non plus de la
base dans laquelle on écrit la famille
. Ce rang ne dépend pas non plus de la
base dans laquelle on écrit la famille
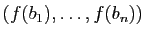 à l'arrivée : c'est le rang des vecteurs colonnes de la matrice de
à l'arrivée : c'est le rang des vecteurs colonnes de la matrice de
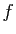 , quelles que soient les bases par rapport auxquelles on écrit
cette matrice.
, quelles que soient les bases par rapport auxquelles on écrit
cette matrice.
Définition 7
Soit
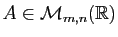 une matrice. On appelle rang de
la matrice
une matrice. On appelle rang de
la matrice 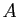 la dimension du sous-espace vectoriel (de
la dimension du sous-espace vectoriel (de
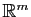 )
engendré par ses vecteurs colonnes.
)
engendré par ses vecteurs colonnes.
Observons que la connaissance du rang fournit un critère
d'inversibilité.
Proposition 7
Une matrice de
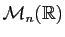 est inversible si et seulement si
son rang est
est inversible si et seulement si
son rang est 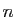 .
.
Démonstration : D'après la proposition 5, une matrice est
inversible, si et seulement si elle représente une application
linéaire bijective de
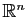 dans lui-même. Or
une application linéaire est bijective
si et seulement si l'image qu'elle donne d'une base est une base,
c'est-à-dire si son rang est
dans lui-même. Or
une application linéaire est bijective
si et seulement si l'image qu'elle donne d'une base est une base,
c'est-à-dire si son rang est 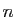 .
. 
Le rang d'une matrice est
celui des applications linéaires qu'elle représente, qui ne
dépend pas des bases. Si deux matrices représentent la même
application dans des bases différentes, elles auront nécessairement
même rang. Rappelons (définition 6
et théorème 3)
que deux matrices sont équivalentes si elles
représentent la même application linéaire dans deux bases
différentes, ou encore si on déduit l'une de l'autre en
multipliant à gauche ou à droite par une matrice inversible.
Deux matrices équivalentes ont même rang. Nous allons démontrer
la réciproque.
Théorème 4
Deux matrices de
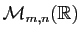 sont équivalentes si et
seulement si elles ont même rang.
sont équivalentes si et
seulement si elles ont même rang.
Démonstration : Nous devons démontrer que deux matrices ayant le même rang sont
équivalentes.
Soit 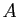 une matrice à
une matrice à 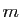 lignes,
lignes, 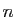 colonnes, et de rang
colonnes, et de rang
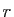 . Notons
. Notons
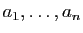 les
les 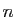 vecteurs colonnes de
vecteurs colonnes de 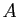 , qui
sont des vecteurs de
, qui
sont des vecteurs de
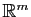 . Le
rang de
. Le
rang de 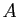 est la dimension de l'espace engendré par
est la dimension de l'espace engendré par
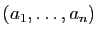 , qui est inférieure ou égale à
, qui est inférieure ou égale à 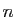 et à
et à 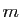 . Nous allons
montrer que la matrice
. Nous allons
montrer que la matrice 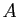 est équivalente à la matrice
est équivalente à la matrice 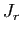 obtenue en complétant la matrice identité
obtenue en complétant la matrice identité 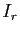 par des
zéros, à droite et en dessous.
par des
zéros, à droite et en dessous.
Considérons l'application 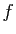 , de
, de
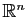 dans
dans
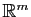 dont la
matrice relative aux bases canoniques est
dont la
matrice relative aux bases canoniques est 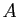 .
Nous voulons trouver une base de l'espace de départ et une
base de l'espace d'arrivée, telles que la matrice de
.
Nous voulons trouver une base de l'espace de départ et une
base de l'espace d'arrivée, telles que la matrice de 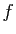 relative
à ces bases soit
relative
à ces bases soit 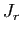 .
.
Comme la dimension de l'image de 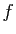 est
est
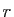 , la dimension du noyau est
, la dimension du noyau est 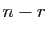 , d'après le théorème du
rang. Soit
, d'après le théorème du
rang. Soit
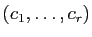 une base de
Im
une base de
Im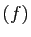 et
et
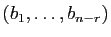 une base de
Ker
une base de
Ker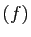 . Pour tout
. Pour tout
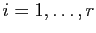 , choisissons un vecteur
, choisissons un vecteur 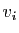 tel que
tel que
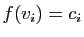 . La
famille
. La
famille
est une base de  : ceci a été établi dans la
démonstration du théorème du rang.
: ceci a été établi dans la
démonstration du théorème du rang.
Dans l'espace d'arrivée  , la famille
, la famille
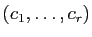 est une
famille libre car c'est une base de
Im
est une
famille libre car c'est une base de
Im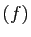 . On peut la
compléter par
. On peut la
compléter par 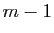 vecteurs
vecteurs
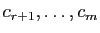 de sorte que
de sorte que
soit une base de 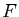 .
.
Pour
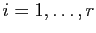 , l'image de
, l'image de 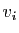 est
est
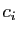 . Les images de
. Les images de
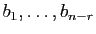 sont nulles : la matrice de
sont nulles : la matrice de
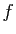 relative aux bases
relative aux bases
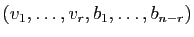 (au
départ) et
(au
départ) et
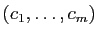 (à l'arrivée) est la matrice
(à l'arrivée) est la matrice 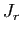 .
.
Puisque 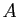 et
et 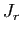 sont équivalentes, il existe deux matrices
inversibles
sont équivalentes, il existe deux matrices
inversibles 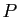 et
et 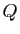 telles que
telles que
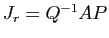 , et donc
, et donc
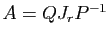 . Soit
. Soit 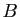 une
autre matrice de
une
autre matrice de
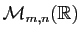 , également de rang
, également de rang 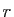 . Il
existe deux autres matrices inversibles
. Il
existe deux autres matrices inversibles 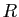 et
et 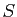 telles que
telles que
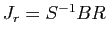 . En multipliant à gauche par
. En multipliant à gauche par 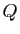 et à droite par
et à droite par
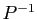 , on obtient :
, on obtient :
Donc deux matrices de même taille et de même rang sont équivalentes.
On déduit de la démonstration qui précède que 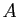 et
et 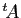 ont le même rang.
ont le même rang.
Démonstration : Nous avons démontré qu'une matrice 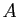 de rang
de rang 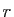 est
équivalente à la matrice
est
équivalente à la matrice 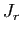 obtenue en complétant
obtenue en complétant 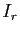 par
des zéros. Or
par
des zéros. Or 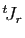 est du même type que
est du même type que 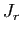 : elle
contient la matrice identité
: elle
contient la matrice identité 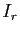 , complétée par des
zéros. Elle est aussi de rang
, complétée par des
zéros. Elle est aussi de rang 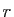 . Par la proposition
2, si
. Par la proposition
2, si
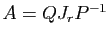 ,
la transposée de
,
la transposée de 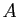 s'écrit :
s'écrit :
Par la proposition 2, la transposée d'une
matrice inversible est inversible. Nous avons donc montré que
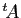 est équivalente à
est équivalente à 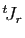 , qui est de rang
, qui est de rang 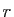 .
.
Déterminer le rang d'une matrice consiste à déterminer le rang
de ses vecteurs colonnes, ou encore de ses vecteurs lignes, puisque ce
sont les colonnes de la transposée. Pour ce faire, nous avons vu une
méthode consistant à écrire un système homogène, puis
à lui appliquer la méthode de Gauss.
Soit
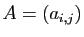 une matrice à
une matrice à 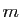 lignes et
lignes et 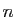 colonnes.
colonnes.
Munissons
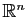 et
et
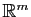 de leurs bases canoniques, et notons
de leurs bases canoniques, et notons 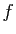 l'application linéaire de
l'application linéaire de
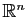 dans
dans
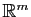 qui a pour matrice
qui a pour matrice
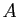 relativement à ces bases. L'application
linéaire
relativement à ces bases. L'application
linéaire 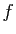 peut être caractérisée de deux façons
différentes.
peut être caractérisée de deux façons
différentes.
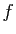 est l'application qui à un
est l'application qui à un 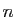 -uplet
-uplet
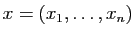 associe le
associe le 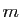 -uplet
-uplet 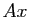 , dont la
, dont la 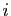 -ième coordonnée vaut
-ième coordonnée vaut
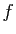 est l'application qui au
est l'application qui au 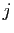 -ième vecteur de la base canonique
de
-ième vecteur de la base canonique
de
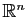 associe le
associe le 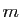 -uplet
-uplet
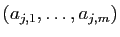 , à savoir
le
, à savoir
le 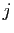 -ième vecteur colonne de
-ième vecteur colonne de 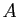 .
.
Le noyau de 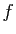 est l'ensemble des
est l'ensemble des 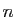 -uplets
-uplets
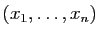 , solutions du système homogène
, solutions du système homogène  suivant.
suivant.
Le rang de ce système est égal à la fois au
rang de 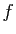 , au rang de
, au rang de 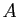 , au
rang de la famille des vecteurs colonnes de
, au
rang de la famille des vecteurs colonnes de 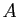 et au rang de la
famille des vecteurs lignes. Pour le
calculer, il suffit de mettre le système
et au rang de la
famille des vecteurs lignes. Pour le
calculer, il suffit de mettre le système  sous forme
échelonnée : le rang est le nombre de pivots non nuls de la forme
échelonnée. On peut aussi déduire de la forme échelonnée une
base de l'image, c'est-à-dire une base de l'espace engendré par
les vecteurs colonnes de
sous forme
échelonnée : le rang est le nombre de pivots non nuls de la forme
échelonnée. On peut aussi déduire de la forme échelonnée une
base de l'image, c'est-à-dire une base de l'espace engendré par
les vecteurs colonnes de 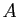 . Il n'est pas indispensable de passer par le
système
. Il n'est pas indispensable de passer par le
système  pour cela. On peut très bien appliquer la méthode
du pivot de Gauss en transformant la matrice
pour cela. On peut très bien appliquer la méthode
du pivot de Gauss en transformant la matrice 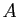 , sans écrire le
système. Ceci revient à remplacer à chaque étape une matrice
par une autre matrice telle que le noyau de l'application linéaire
associée soit le même : le rang n'est donc pas modifié.
Voici un exemple.
Considérons la matrice
suivante.
, sans écrire le
système. Ceci revient à remplacer à chaque étape une matrice
par une autre matrice telle que le noyau de l'application linéaire
associée soit le même : le rang n'est donc pas modifié.
Voici un exemple.
Considérons la matrice
suivante.
Le coefficient d'ordre 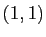 est non nul, il n'y a donc pas de
permutations à effectuer. Le premier pivot est
est non nul, il n'y a donc pas de
permutations à effectuer. Le premier pivot est 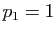 . Voici les
transformations qui annulent la première colonne au-dessous du pivot.
. Voici les
transformations qui annulent la première colonne au-dessous du pivot.
Le second pivot est 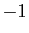 . Les transformations qui annulent le bas de la
seconde colonne sont les suivantes.
. Les transformations qui annulent le bas de la
seconde colonne sont les suivantes.
Pour obtenir un troisième pivot non nul, il faut échanger les deux
dernières colonnes.
Le troisième pivot est 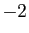 . Il ne reste qu'une ligne à transformer.
. Il ne reste qu'une ligne à transformer.
Le rang de la matrice est donc 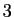 . En n'oubliant pas que les colonnes
. En n'oubliant pas que les colonnes
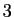 et
et 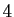 ont été échangées, on obtient aussi
que les vecteurs colonnes numéros
ont été échangées, on obtient aussi
que les vecteurs colonnes numéros 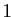 ,
, 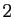 et
et 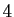 de la matrice
de la matrice 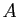 forment une famille libre, donc une base de l'espace engendré.
Bien que l'écriture du système soit mathématiquement superflue,
elle est techniquement plus sûre, et nous vous conseillons de la
conserver.
forment une famille libre, donc une base de l'espace engendré.
Bien que l'écriture du système soit mathématiquement superflue,
elle est techniquement plus sûre, et nous vous conseillons de la
conserver.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![\begin{displaymath}
J_r =
\begin{array}{c\vert c}
\left.
\begin{array}{cccccccc}...
...15ex]
r+1\ [0.15ex]
\vdots\ [0.15ex]
m
\end{array}\end{array}\end{displaymath}](img187.gif)
![]() est
est
![]() , la dimension du noyau est
, la dimension du noyau est ![]() , d'après le théorème du
rang. Soit
, d'après le théorème du
rang. Soit
![]() une base de
Im
une base de
Im![]() et
et
![]() une base de
Ker
une base de
Ker![]() . Pour tout
. Pour tout
![]() , choisissons un vecteur
, choisissons un vecteur ![]() tel que
tel que
![]() . La
famille
. La
famille
![]() , la famille
, la famille
![]() est une
famille libre car c'est une base de
Im
est une
famille libre car c'est une base de
Im![]() . On peut la
compléter par
. On peut la
compléter par ![]() vecteurs
vecteurs
![]() de sorte que
de sorte que
![]() , l'image de
, l'image de ![]() est
est
![]() . Les images de
. Les images de
![]() sont nulles : la matrice de
sont nulles : la matrice de
![]() relative aux bases
relative aux bases
![]() (au
départ) et
(au
départ) et
![]() (à l'arrivée) est la matrice
(à l'arrivée) est la matrice ![]() .
.
![]() et
et ![]() sont équivalentes, il existe deux matrices
inversibles
sont équivalentes, il existe deux matrices
inversibles ![]() et
et ![]() telles que
telles que
![]() , et donc
, et donc
![]() . Soit
. Soit ![]() une
autre matrice de
une
autre matrice de
![]() , également de rang
, également de rang ![]() . Il
existe deux autres matrices inversibles
. Il
existe deux autres matrices inversibles ![]() et
et ![]() telles que
telles que
![]() . En multipliant à gauche par
. En multipliant à gauche par ![]() et à droite par
et à droite par
![]() , on obtient :
, on obtient :
![]() et
et ![]() ont le même rang.
ont le même rang.
![]() une matrice à
une matrice à ![]() lignes et
lignes et ![]() colonnes.
colonnes.
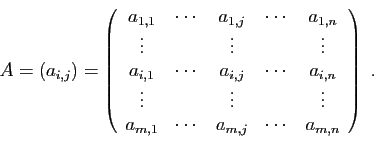
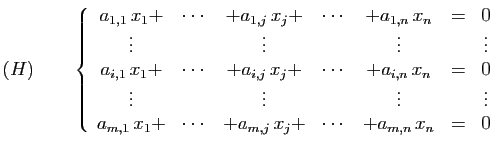
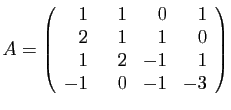
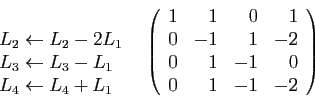
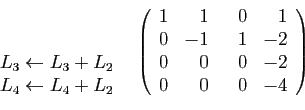
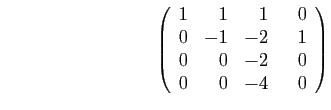
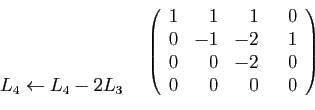
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales