Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit
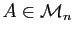 une matrice carrée. On note
une matrice carrée. On note 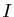 la matrice
identité de dimension
la matrice
identité de dimension 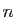 . On suppose qu'il existe une matrice
. On suppose qu'il existe une matrice 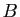 telle que
telle que 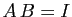 .
.
- Soit
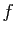 l'application de
l'application de
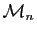 dans
dans
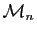 qui à une
matrice
qui à une
matrice 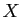 associe le produit
associe le produit 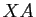 . Montrer que
. Montrer que 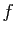 est une
application linéaire.
est une
application linéaire.
- Montrer que
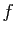 est injective. En déduire que
est injective. En déduire que 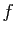 est bijective.
est bijective.
- Montrer qu'il existe une matrice
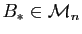 telle que
telle que
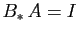 . Montrer que
. Montrer que 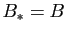 . En déduire que
. En déduire que 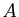 est inversible.
est inversible.
- Soit
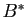 une matrice telle que
une matrice telle que 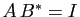 . Montrer que
. Montrer que
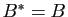 .
.
- Soit
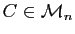 une autre matrice inversible. Montrer que le
produit
une autre matrice inversible. Montrer que le
produit 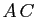 est inversible et que
est inversible et que
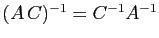 .
.
Exercice 1 :
Soient 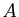 et
et 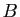 les deux matrices suivantes.
les deux matrices suivantes.
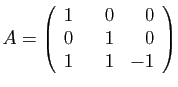
et
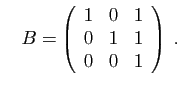
- Vérifier que
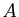 est inversible et calculer
est inversible et calculer 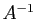 .
.
- Vérifier que
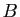 est inversible et calculer
est inversible et calculer 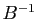 .
.
- On pose
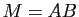 . Justifier le fait que
. Justifier le fait que 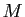 est inversible et calculer
est inversible et calculer
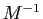 , en utilisant les résultats des deux questions
précédentes.
Dans toute la suite,
, en utilisant les résultats des deux questions
précédentes.
Dans toute la suite,
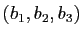 désigne une base de
désigne une base de
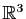 . On note
. On note 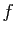 (respectivement :
(respectivement : 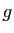 ) l'application de
) l'application de
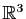 dans lui-même qui a pour matrice
dans lui-même qui a pour matrice 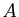 (respectivement :
(respectivement : 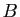 ) dans la
base
) dans la
base
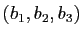 .
.
- Exprimer en fonction de
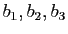 les vecteurs
les vecteurs
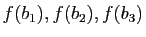 , puis
, puis
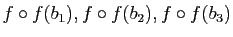 . Retrouver le résultat de la question 1.
. Retrouver le résultat de la question 1.
- Exprimer les vecteurs
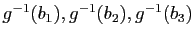 en fonction de
en fonction de
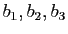 .
.
- On note
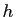 l'application linéaire de
l'application linéaire de
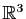 dans lui-même, qui
à un vecteur
dans lui-même, qui
à un vecteur 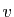 associe
associe
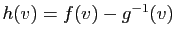 . Ecrire la matrice de
. Ecrire la matrice de
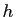 dans la base
dans la base
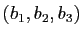 .
.
- Donner, en fonction de
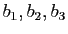 , une base de
, une base de
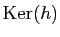 et
une base de
et
une base de
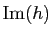 .
.
- On note
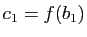 ,
,
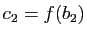 ,
,
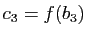 . Montrer que
. Montrer que
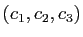 est une base de
est une base de
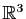 . Quelle est la matrice de
l'application
. Quelle est la matrice de
l'application 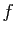 dans la base
dans la base
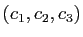 ?
?
- Calculer les matrices des applications
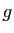 et
et 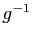 dans la base
dans la base
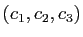 .
.
Exercice 2 :
Soient 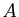 et
et 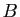 les deux matrices suivantes.
les deux matrices suivantes.
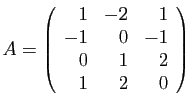
et
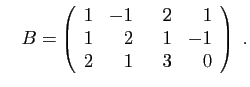
On note 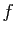 l'application de
l'application de
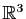 dans
dans
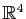 qui a pour matrice
qui a pour matrice
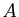 relativement aux bases canoniques, et
relativement aux bases canoniques, et 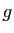 l'application de
l'application de
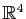 dans
dans
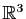 qui a pour matrice
qui a pour matrice 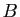 relativement aux bases canoniques.
relativement aux bases canoniques.
- Calculer les produits
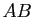 et
et 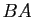 .
.
- On note
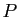 la matrice constituée des trois premières lignes de la
matrice
la matrice constituée des trois premières lignes de la
matrice 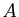 . Vérifier que
. Vérifier que 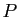 est inversible et calculer son
inverse. En déduire le rang de la matrice
est inversible et calculer son
inverse. En déduire le rang de la matrice 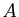 .
.
- Déterminer le rang de
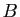 .
En déduire le rang des matrices
.
En déduire le rang des matrices 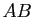 et
et 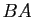 .
.
- On note
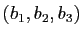 les trois vecteurs
colonnes de la matrice
les trois vecteurs
colonnes de la matrice 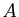 . Soit
. Soit
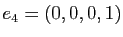 le quatrième
vecteur de la base canonique de
le quatrième
vecteur de la base canonique de
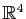 . Justifier le fait
que
. Justifier le fait
que
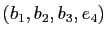 est une base de
est une base de
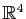 .
.
- Donner la matrice de l'application
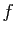 ,
relative à la base canonique de
,
relative à la base canonique de
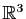 au départ
et à la base
au départ
et à la base
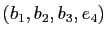 à l'arrivée.
à l'arrivée.
- Calculer la matrice de l'application
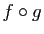 dans la base
dans la base
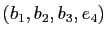 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() une matrice carrée. On note
une matrice carrée. On note ![]() la matrice
identité de dimension
la matrice
identité de dimension ![]() . On suppose qu'il existe une matrice
. On suppose qu'il existe une matrice ![]() telle que
telle que ![]() .
.
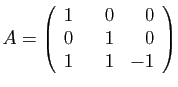 et
et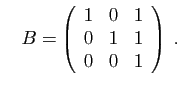
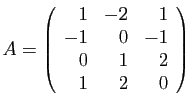 et
et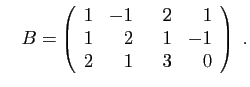
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales