Par définition si 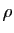 et
et 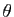 désignent respectivement le module et l'argument du nombre complexe
désignent respectivement le module et l'argument du nombre complexe
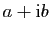 , alors
, alors
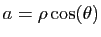 et
et
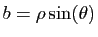 . Ainsi
le nombre s'écrit :
. Ainsi
le nombre s'écrit :
On dit que le nombre est mis sous forme trigonométrique,
ou forme polaire.
Cette écriture prend toute sa force
grâce à l'exponentielle complexe.
Observez que l'exponentielle complexe coïncide avec
l'exponentielle réelle si la partie imaginaire est nulle. Si la
partie réelle est nulle, le nombre
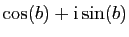 est un nombre
complexe de module
est un nombre
complexe de module 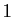 (car
(car
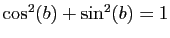 ).
Dans le cas général, le module de
).
Dans le cas général, le module de
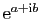 est
est
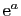 et son argument est l'unique élément
et son argument est l'unique élément 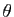 de
de  tel que
tel que 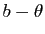 soit multiple de
soit multiple de 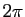 .
.
La périodicité modulo 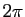 des fonctions sinus et cosinus
induit la périodicité modulo
des fonctions sinus et cosinus
induit la périodicité modulo
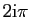 de l'exponentielle complexe :
pour tout réel
de l'exponentielle complexe :
pour tout réel 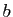 et pour tout entier
et pour tout entier 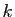 ,
,
Ainsi,
L'exponentielle complexe conserve la propriété fondamentale de
l'exponentielle réelle qui
est de transformer les sommes en produits.
Démonstration : Posons
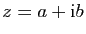 et
et
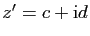 . Par définition de l'exponentielle,
. Par définition de l'exponentielle,
D'autre part,
car
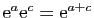 (propriété de l'exponentielle réelle).
Les formules trigonométriques suivantes sont supposées connues:
(propriété de l'exponentielle réelle).
Les formules trigonométriques suivantes sont supposées connues:
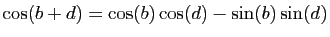
et
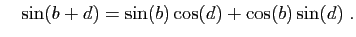
On en déduit immédiatement que :

Si 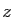 est un nombre complexe de module
est un nombre complexe de module 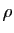 et d'argument
et d'argument 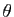 ,
il est souvent commode de l'écrire sous sa forme
exponentielle :
,
il est souvent commode de l'écrire sous sa forme
exponentielle :
Observez que le conjugué est :
et son argument est
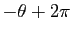 .
L'utilisation de l'exponentielle facilite le calcul des produits et
des puissances. Par exemple si
.
L'utilisation de l'exponentielle facilite le calcul des produits et
des puissances. Par exemple si 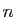 est un entier,
est un entier,
Il est facile également de retrouver les racines 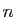 -ièmes d'un
nombre complexe sous forme trigonométrique, c'est-à-dire de
résoudre l'équation
-ièmes d'un
nombre complexe sous forme trigonométrique, c'est-à-dire de
résoudre l'équation
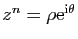 . Il y a
. Il y a 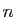 solutions
qui s'écrivent :
solutions
qui s'écrivent :
Les nombres de la forme
sont les solutions de 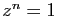 . On les appelle les
racines
. On les appelle les
racines 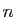 -ièmes de l'unité (figure 4).
-ièmes de l'unité (figure 4).
Figure 4:
Racines douzièmes de l'unité.
|
|
Les fonctions sinus et cosinus s'expriment à l'aide de
l'exponentielle complexe par les formules d'Euler.
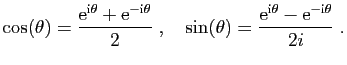 |
(7) |
On les utilise pour linéariser des puissances de sinus et
cosinus, afin de calculer leurs primitives. Voici un exemple.
D'où une primitive de
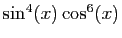 :
:
L'observation de la parité permet de prévoir a
priori que la linéarisation ne contiendra que des 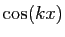 . En
effet,
. En
effet, 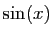 est une fonction impaire et
est une fonction impaire et 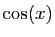 une fonction
paire. Donc si on remplace
une fonction
paire. Donc si on remplace 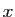 par
par 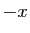 ,
,
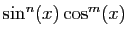 sera
inchangé si
sera
inchangé si 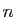 est pair, changé en son opposé si
est pair, changé en son opposé si 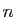 est
impair. Dans le premier cas, la linéarisation ne contiendra que des
cosinus, dans le second cas, elle ne contiendra que des sinus.
est
impair. Dans le premier cas, la linéarisation ne contiendra que des
cosinus, dans le second cas, elle ne contiendra que des sinus.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() des fonctions sinus et cosinus
induit la périodicité modulo
des fonctions sinus et cosinus
induit la périodicité modulo
![]() de l'exponentielle complexe :
pour tout réel
de l'exponentielle complexe :
pour tout réel ![]() et pour tout entier
et pour tout entier ![]() ,
,
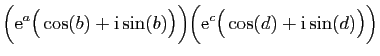
![]() est un nombre complexe de module
est un nombre complexe de module ![]() et d'argument
et d'argument ![]() ,
il est souvent commode de l'écrire sous sa forme
exponentielle :
,
il est souvent commode de l'écrire sous sa forme
exponentielle :
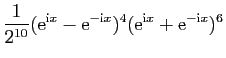
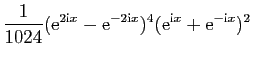
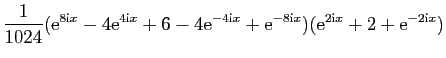
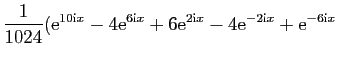
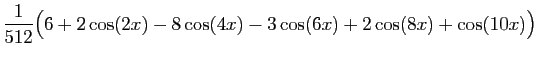
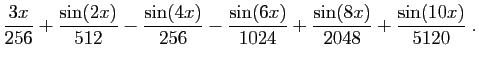
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales