 |
|
Ibrahim Cheddadi, Pierre Saramito et François Graner
Un article des mêmes auteurs paraîtra prochainement dans la revue Pour la science. Cet article en partage certaines parties tout en développant spécifiquement les aspects les plus mathématiques.
Il est question ici de la modélisation mathématique des mousses liquides sous la forme d'un milieu continu. Les équations décrivant le comportement de ces milieux complexes sont nouvelles et soulèvent des questions tant au niveau théorique qu'à celui du calcul par ordinateur.
Mettez un peu d'eau dans une bouteille, ajoutez quelques gouttes de liquide vaisselle, agitez : la mousse se forme. Avez-vous déjà essayé de la rincer ? Connaissez vous rien de plus agaçant ? Cette écume, apparemment fugace et molle, résiste obstinément à toute tentative de la faire s'écouler à travers le goulot. Voyons de plus près ce mystère, qui n'a que très récemment pu être décrit par des équations mathématiques.
Facile à fabriquer et peu coûteuse, la mousse de savon s'est imposée comme système modèle dans les laboratoires de physique pour des disciplines variées. Voici un écoulement de mousse, numérisé par tomographie aux rayons X :
 |
|
Les mathématiciens, bien que moins enclins que les physiciens à s'appuyer sur des expériences, ont reconnu dans les films d'eau savonneuse des objets qui minimisent leur surface : en effet, la surface entre l'eau et l'air est tendue [13,8]. Ainsi, Richard Courant, étudiant les surfaces minimales, a été photographié dans les années 1950 lors d'une séance de démonstration de films d'eau savonneuse devant ses collaborateurs [1]. Richard Courant a contribué de façon importante aux mathématiques, notamment sur les méthodes d'approximation des solutions des équations complexes. Un célèbre institut de mathématiques new-yorkais porte aujourd'hui son nom [1].

|
Les observations des tissus biologiques faits de cellules, de A. Leeuwenhoek au XVIIè siècle à d'Arcy Thomson au XIXè siècle, ont souligné l'analogie avec les mousses : les bulles et les cellules ont des propriétés très différentes, mais leurs façons de s'assembler qui présentent de réels points communs. Cette analogie avec les mousses liquides n'est pas la seule. Les métallurgistes savent que les propriétés d'un acier dépendent fortement de sa structure en petits grains cristallins, structure qui évolue dans le temps en vieillissant [21]. Dans les années 1950, Cyril S. Smith a mis en évidence une analogie très précise avec le vieillissement de la mousse de savon, avec l'aide du mathématicien John von Neumann. Il est plus facile d'observer une mousse de savon à l'œil nu qu'un acier au microscope : il a su exploiter cette analogie pour mieux comprendre le vieillissement des aciers.Enfin, les artistes ne sont pas en reste ; d'un tableau de Chardin à un opéra contemporain dansé sur une scène remplie de mousse, des bulles géantes d'un clown jusqu'aux installations de sculptures de mousse, la coopération entre art et physico-chimie a trouvé de quoi se nourrir au milieu de couleurs irisées.
La mousse est également très utile en tant que telle. Dans la vie quotidienne, la mousse est en général un élément de confort ou de plaisir, par exemple la mousse de la bière et la mousse à raser, ou encore pour les mousses alimentaires, les cosmétiques et le nettoyage domestique. L'application la plus connue du grand public est sans doute la mousse des extincteurs et des pompiers : contrairement à l'eau, la mousse est plus légère que l'huile, ce qui la rend efficace sur un feu de pétrole. Les applications industrielles tirent parti des différents avantages de la mousse. En terme de tonnage, ce sont les mines qui emploient le plus de mousse, pour séparer les minerais utiles de la gangue inutile. L'industrie pétrolière aussi en utilise massivement, tant pour le forage que pour l'extraction. Des dizaines d'autres créneaux plus spécifiques vont de l'amortissement des chocs à la fracturation des roches, en passant par l'injection de médicaments dans les veines.
Ces applications font appel aux propriétés complexes d'écoulement de la mousse, sur lesquelles se penchent les laboratoires de recherche. Ici encore, ils seront rejoints par des chercheurs d'autres domaines. Dans ce type d'études interdisciplinaires, les mathématiciens et les physiciens collaborent de façon étroite, dans un domaine dit des fluides complexes. Ce domaine recouvre également les émulsions (par exemple, la mayonnaise), les polymères fondus ou en solution (matières plastiques) ou encore les laves volcaniques.
Plutôt que de décrire tous les événements individuels un à un, nous cherchons une description mathématique directe du comportement macroscopique complexe émergeant : cette description est appelée représentation continue.
Pour des systèmes physiques plus simples, nous savons partir des équations décrivant les comportements à des petites échelles et remonter à des équations décrivant complètement le comportement macroscopique, à grande échelle. Par exemple, pour des gaz peu denses composés de sphères dures en interaction, nous savons obtenir les équations dites de Boltzmann [16], qui décrivent ce gaz à grande échelle, comme un milieu continu et non plus comme un assemblage de sphères. Pour ces équations, un appareil mathématique considérable a été développé pour donner un cadre rigoureux à ce passage des petites aux grandes échelles. Cette théorie a connu des développements impressionnants, en particulier en France où deux mathématiciens travaillant dans ce domaine, P. L. Lions et C. Villani [15], ont reçu la médaille Fields. Lorsque le gaz se densifie, les équations de Boltzmann conduisent à celles de Navier-Stokes [9], qui décrivent un fluide composé de sphères dures en interaction. Par une représentation continue, ces équations décrivent par exemple l'air ou l'eau, et sont utiles pour de nombreuses applications telles que l'aéronautique, l'océanographie, la prévision météo ou celle des changements climatiques. La théorie relative à l'existence et l'unicité des solutions des équations de Navier-Stokes n'est pas encore aboutie [17] : il s'agit du sixième problème du prix du millénaire [14]. Ainsi, même pour des fluides simples, il est encore délicat aujourd'hui d'établir le lien entre micro et macro structure, ici entre des sphères discrètes et un milieu continu.
Lorsque la microstructure est plus complexe que des sphères dures en interaction, le fluide est dit complexe. Pour certaines solutions de polymères, qui constituent déjà des fluides complexes, il est possible d'obtenir un système d'équations fermés pour l'écoulement macroscopique du fluide à partir d'une description mathématique du comportement des macro-molécules de polymères à l'échelle microscopique. Ainsi, à partir des interactions de polymères en forme d'haltères suspendus dans un solvant, il est possible de montrer que l'on retrouve au niveau macro, et dans le cadre d'un milieu continu, un modèle visco-élastique dit d'Oldroyd [2].
La méthodologie qui consiste à s'appuyer sur des hypothèses issues d'observations physiques pour passer du système discret, ici l'assemblage des bulles, à une représentation continue, est similaire pour l'étude d'autres systèmes complexes comme les tissus biologiques, les bancs de poissons, les fourmis, les foules ou la circulation automobile [6].
Dans le cas des mousses liquides, la situation est particulièrement délicate : nous manquions jusqu'à récemment d'un système d'équations décrivant l'échelle macroscopique. Les travaux ont avancé en plusieurs étapes successives. Au niveau macro, la compréhension des mécanismes physiques à l'œuvre est relativement bien établie pour une mousse qui ne bouge pas, à l'équilibre. Le lien entre la molécule et le film d'eau savonneuse a bénéficié des progrès de la physico-chimie, en particulier de l'école bulgare [7] durant ces dernières décennies, aboutissant à des procédures de fabrication stables, reproductibles et modulables à la demande. Durant les années 1980 à 2000, a été compris le lien entre le film d'eau savonneuse et la bulle, dominé par les phénomènes de capillarité où l'école française s'est beaucoup impliquée [11,3]. En parallèle, a été établi le lien entre la bulle et la mousse, où se sont illustrés des physiciens irlandais [19] en collaboration avec des mathématiciens géomètres ou topologues.
À partir des années 2000, l'effort s'est concentré sur un défi lancinant depuis des décennies, celui de décrire une mousse liquide à l'échelle macroscopique, dans le cadre d'un milieu continu, et par un système d'équations. Intuitivement, on sent que la consistance de la mousse, qui contribue grandement à son charme, sort des catégories que l'on enseigne à l'école. Est-elle solide ? Est-elle liquide ? Peut-elle être liquide et solide à la fois ? Si oui, alors qu'est-ce que cela signifie ?
Déposez dans votre main gauche un peu de mousse à raser, en un petit tas pointu. Faites osciller votre main de droite à gauche : la mousse se déforme en oscillant, ce qui signifie que les bulles qui la composent se déforment aussi, même si vous ne le constatez pas à l'œil nu. Quand vous arrêtez les oscillations, la mousse reprend sa forme initiale, car les bulles qui la composent reviennent dans la configuration non déformée, où leur énergie est plus petite. Votre morceau de mousse à raser a ainsi une forme propre, et un comportement réversible. A strictement parler, c'est alors un solide élastique, comme un morceau de caoutchouc. Cette propriété solide est d'autant plus surprenante que, rappelons-le, cette mousse n'est faite que d'un mélange de deux fluides ! En l'occurrence un gaz, l'air des bulles, dispersé dans un liquide, l'eau savonneuse des parois.
Ayez maintenant moins de délicatesse, et appuyez franchement sur la mousse à raser avec votre index droit. Votre doigt s'enfonce, il sculpte la mousse, vous pouvez changer la forme de votre tas. La mousse peut se modeler : c'est ce que signifie le mot plastique, comme peut l'être une boule de pâte à modeler, qui a une forme acquise. Autrement dit, en passant d'une petite déformation à une grande, vous avez fait passer le comportement de la mousse de celui d'un solide élastique à un fluide visco-plastique. On le comprend en observant les réarrangements de bulles : si elles se déforment suffisamment, elles changent de voisins et tombent dans une nouvelle configuration, où des bulles s'éloignent tandis que d'autres se rapprochent.
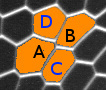 |
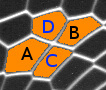 |
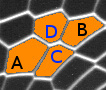 |
|
Au final, la même mousse peut être élastique ou plastique, selon la perturbation que vous lui appliquez. Certes, d'une mousse à l'autre, les propriétés particulières changent. Telle mousse est plus rigide, telle autre mousse tolère des déformations plus grandes, telle mousse enfin casse si on essaie de la déformer trop vite. Ces différences proviennent de la proportion d'eau, de la composition du savon ou de la distribution des tailles des bulles, par exemple. Mais fondamentalement, le comportement élastique ou plastique est lié à la structure même de la mousse, plus précisément à sa nature de matériau cellulaire.
![]()
![]()
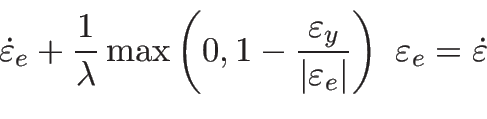
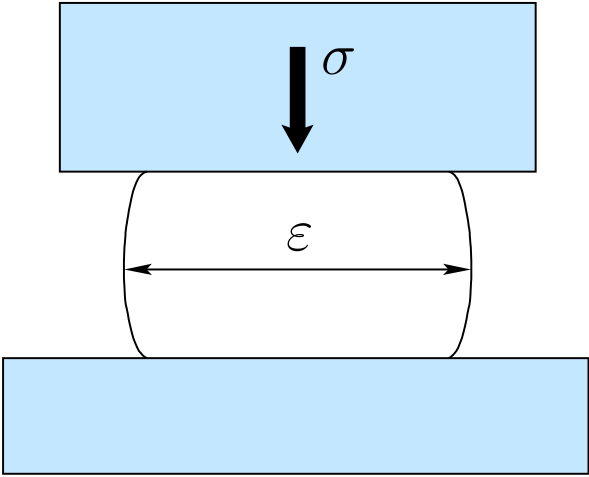
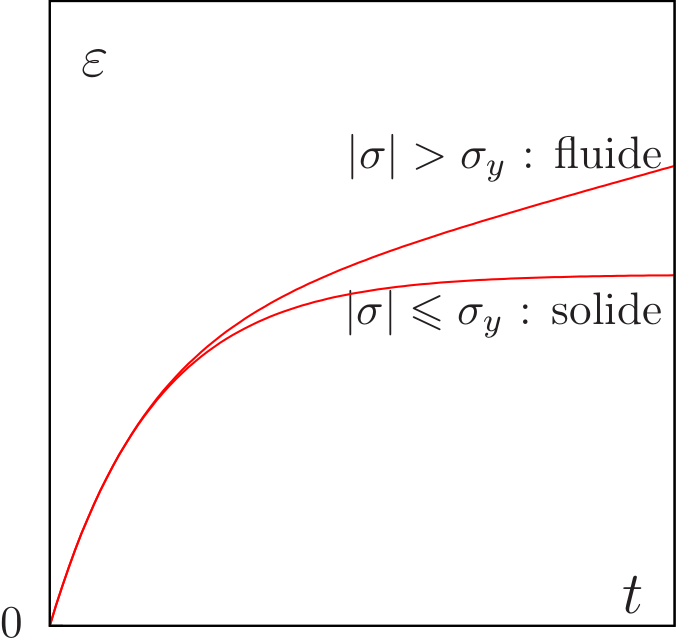
Explorons cette équation par une expérience virtuelle d'aplatissement : exerçons une contrainte σ donnée sur un échantillon d'un matériau décrit par ces trois équations où les déformations (εe, εp, ε) sont les trois inconnues. Observons la déformation ε qui en résulte en fonction du temps t en supposant le matériau initialement au repos (les déformations initiales sont nulles). La résolution du système d'équations différentielles peut s'effectuer explicitement, avec un crayon et un papier [18] et la solution ε est représentée sur la figure suivante :
 |
 |
|
Introduisons σy = Gεy, appelé le seuil de contrainte et qui est une constante positive. Si la force de poussée est faible, | σ|≤σy, la déformation croît et atteint asymptotiquement un plateau : comme pour un morceau de caoutchouc, nous avons affaire à un solide. Si nous nous asseyons sur un pouf, (la contrainte σ représente notre poids), celui-ci va subir une déformation finie. La déformation est réversible : si nous nous levons, la contrainte σ devient nulle et le pouf va, à terme, retrouver sa forme initiale. Si la force de poussée est plus importante et dépasse le seuil, la déformation croît indéfiniment et n'est plus bornée : nous avons affaire à un fluide. Si il s'agit du pouf précédent, nous avons exercé une contrainte trop forte, nous sommes trop lourds ! Ou bien le pouf pas assez résistant... Dans tous les cas, une grande déformation, irréversible pour le pouf, s'est produite : le pouf se retrouve complètement aplati ! Si à présent nous nous levons, il ne retrouvera plus sa forme initiale : la déformation est dite plastique : en quelque sorte, nous avons sculpté le pouf. Ce double comportement ne dépend que des conditions auxquels le matériau est soumis. Cette situation est bien celle de la mousse liquide. Cette équation, somme toute assez simple, sera-t-elle en mesure de décrire les mouvements de la mousse liquide dans des conditions d'écoulement moins triviales que ce simple test d'aplatissement ? Peut-on prédire comment va s'écouler de la mousse, et si oui, de quoi a-t-on besoin pour cela ?
À l'équation de comportement précédente, il faut ajouter deux équations usuelles exprimant la conservation de la masse et de la quantité de mouvement de la mousse au cours du temps. Ces trois équations forment un système dont les trois inconnues sont la déformation élastique εe, la vitesse et la pression, définies à chaque instant et en chaque point du domaine d'écoulement.
Ce système d'équations possède deux paramètres, le temps de relaxation λ et la déformation-seuil εy, qui sont en facteur des deux principales non-linéarités des équations. Ces deux non-linéarités sont les principales sources de difficultés dans la résolution du système d'équations. Lorsque ces deux paramètres sont non-nuls, le matériau est dit élasto-visco-plastique. Lorsque λ = εy = 0, nous retrouvons un matériau simple, comme l'eau, et qu'on appelle un fluide newtonien [20], et le système se réduit aux équations de Navier-Stokes. Lorsque seul λ = 0, nous avons affaire à un fluide visco-plastique, ou fluide à seuil, tels que le dentifrice, la peinture ou la lave volcanique, qui s'écoule dès que l'on applique une force supérieure à un certain seuil. Enfin, lorsque seul εy = 0, nous avons affaire à un fluide visco-élastique, comme la poix ou cette amusante pâte de polymère commercialisée sous le nom de silly putty. Une boule de silly putty rebondit sur le sol et cependant, si on la pose sur une surface horizontale et attend quelques minutes, on la voit s'étaler comme un fluide visqueux.
Contrairement au problème d'aplatissement précédent, dans le cas général, les équations ne peuvent plus être résolues explicitement par une formule. Seules des approximations des solutions peuvent être obtenues par calcul numérique à l'aide d'un ordinateur. La résolution numérique des équations s'est avérée d'une redoutable difficulté : elle a fait l'objet de la thèse [4] de l'un de nous trois (I.C.) sous la direction des deux autres. Elle a requis un soin particulier et surtout de multiples tests de validation, du fait des fortes non-linéarités des équations.
Enfin, nous avons testé la capacité prédictive des équations en comparant les résultats des calculs numériques avec des mesures expérimentales effectuées sur des mousses liquides. Pour cela, nous avons considéré une mousse composée d'une seule couche de bulles, s'écoulant entre deux plaques de verre parallèles et qui rencontre un obstacle circulaire :

|
Les calculs permettent de prédire l'étirement et la direction des bulles, représentés ici sous la formes d'ellipses :
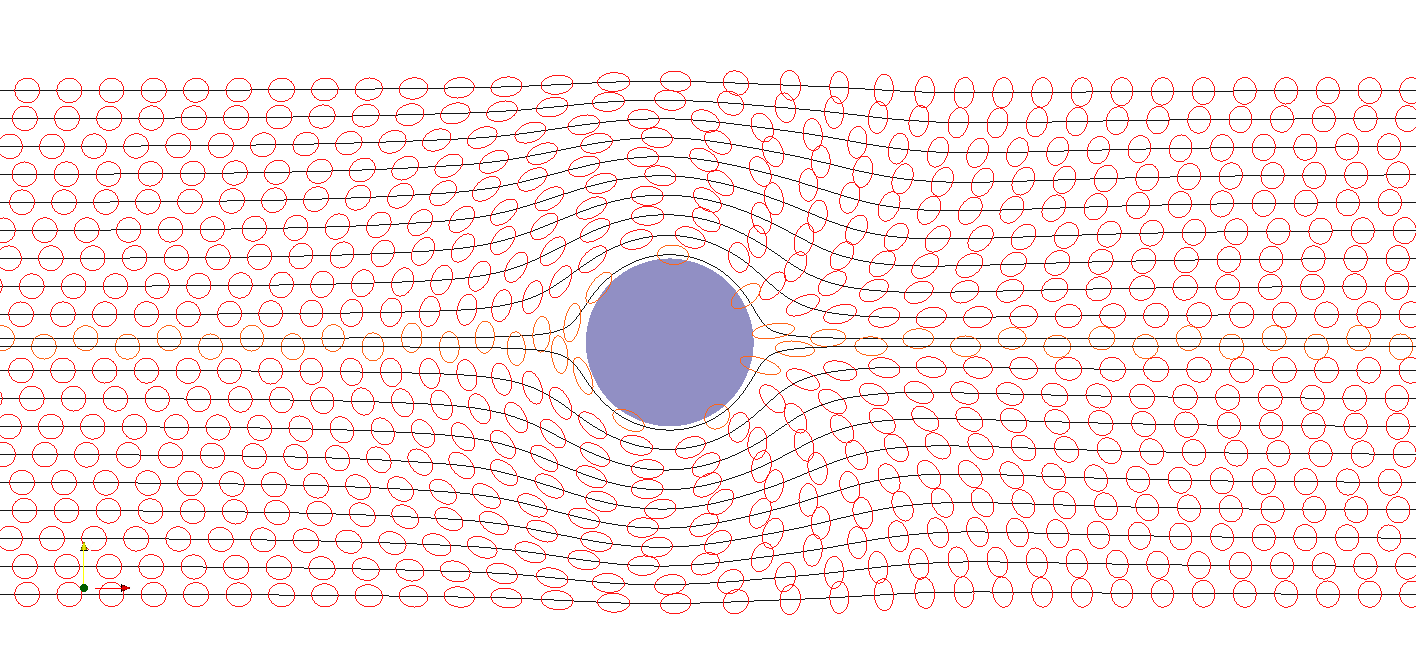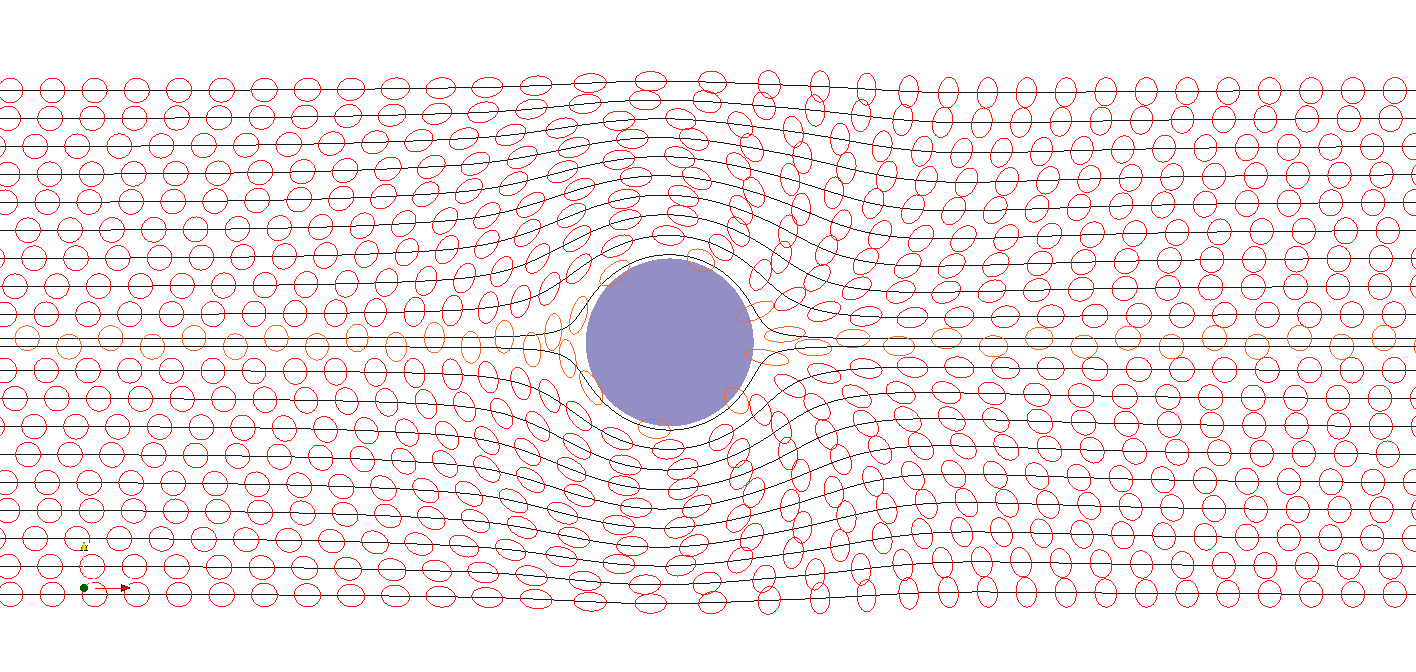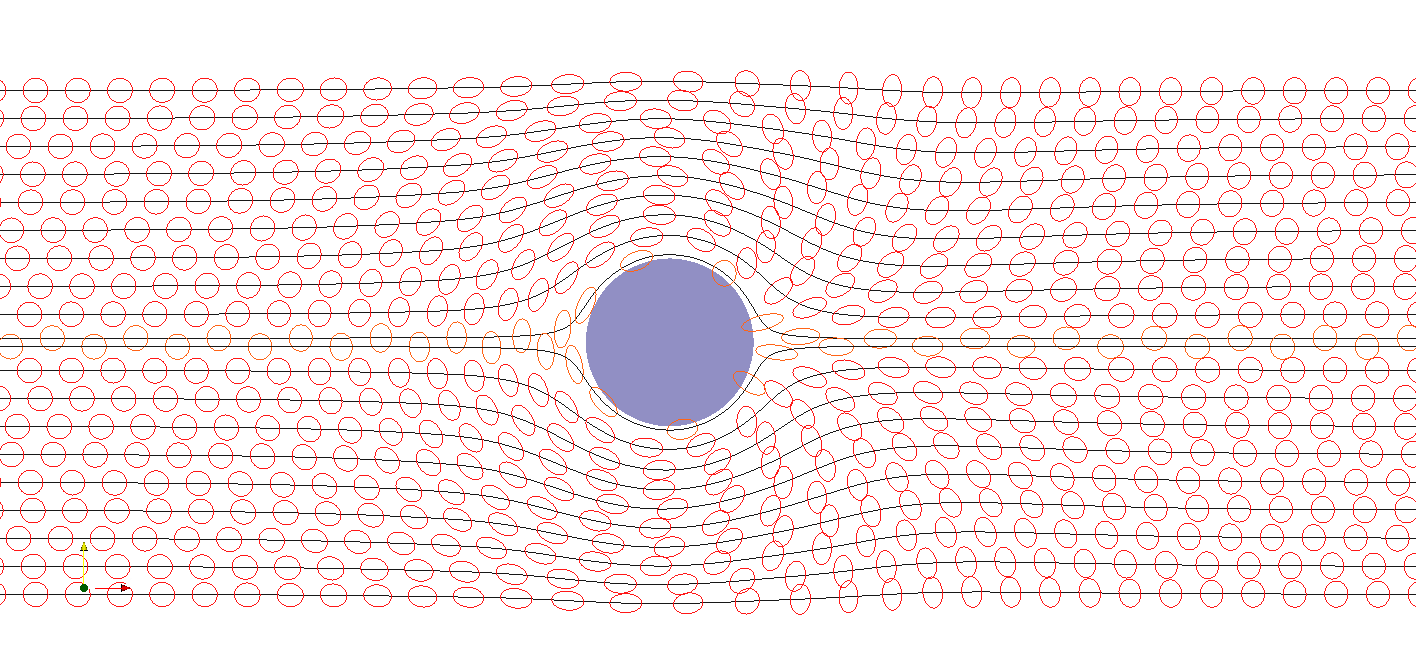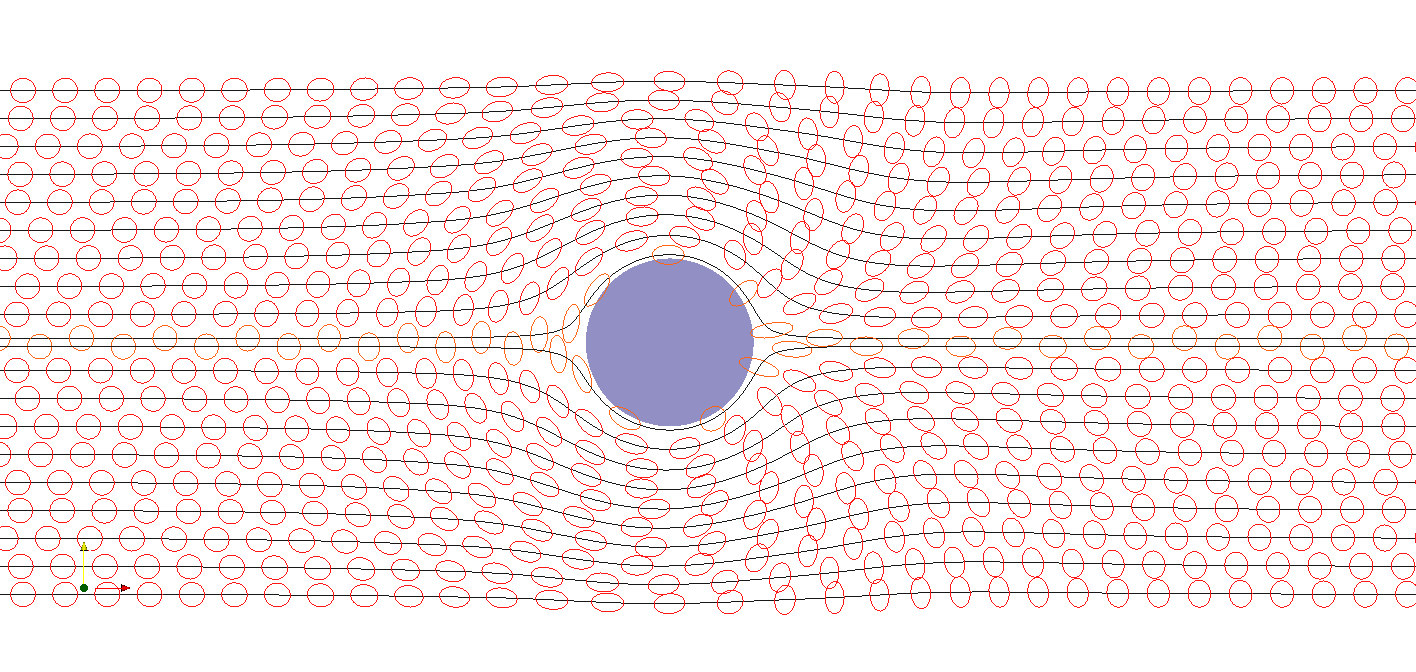
|
Les ellipses de l'animation précédente représentent les formes des bulles qui s'obtiennent à partir du champs de déformation élastique εe. Lorsque le matériau est au repos, la déformation élastique est nulle et l'ellipse se réduit à un cercle. Lorsque le matériau se déforme, l'ellipse s'étire et donne les directions principales de déformation. Ces prédictions semblent qualitativement en bon accord avec les observations que nous pouvons effectuer sur la mousse liquide réelle de la vidéo précédente. Il est possible de confronter prédiction et photographie sur une même figure :
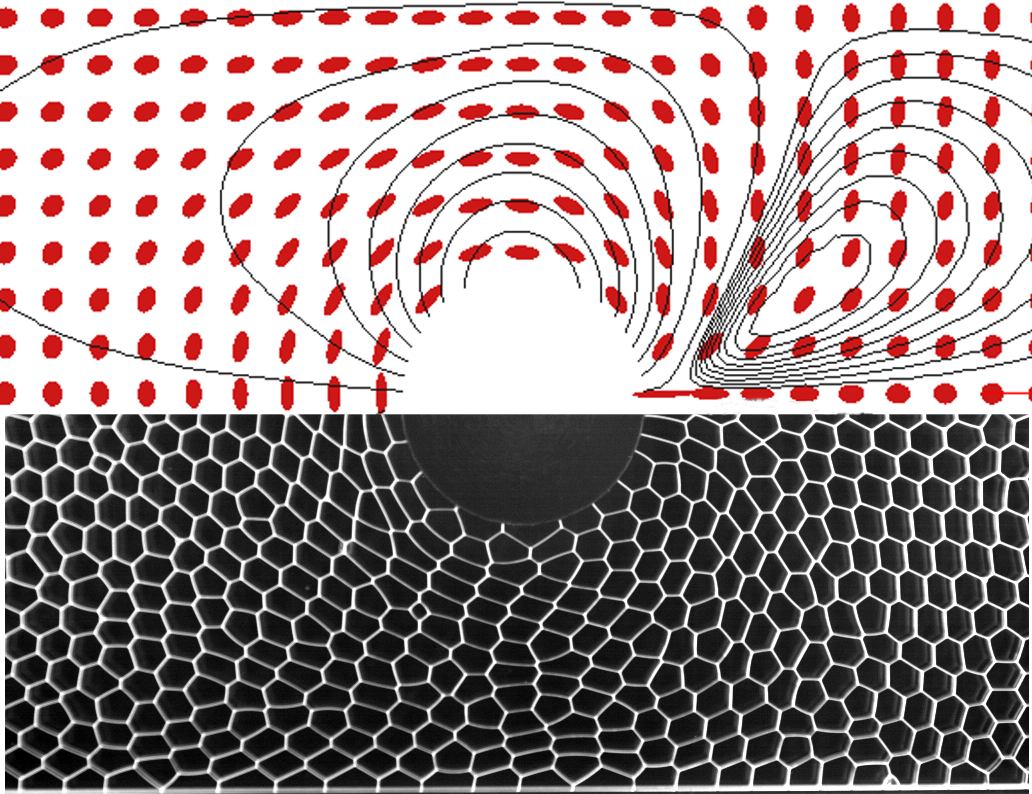
|
Plutôt que d'observer la mousse en restant immobile, observons-là en nous déplaçant avec une vitesse constante, celle de la mousse qui arrive sur l'obstacle. Avec ce point de vue, l'obstacle circulaire semble se déplacer de la droite vers la gauche dans une mousse globalement au repos. Les lignes noires sur la figure précédente sont les trajectoires du matériau ainsi observé : deux recirculations apparaissent, l'une attachée à l'obstacle et l'autre à droite, en aval de celui-ci. Les bulles à gauche de l'obstacle semblent aplaties par l'avancée de celui-ci, alors qu'à droite, à l'arrière de l'obstacle, elles sont plus étirées.
Mais comment obtenir des comparaisons quantitatives, plus précises ? Impossible pour cela de se fier seulement à notre œil, plus attiré par les contours des bulles elles-mêmes et par leurs mouvements que par l'écoulement à grande échelle, et surtout plus habitué à distinguer des structures qu'à comparer des nombres. Dans un travail publié en 2011, les observations expérimentales ont permis d'extraire la vitesse du fluide ainsi que la déformation élastique εe et de comparer ces quantités avec les valeurs prédites par le calcul [5]. Cet accord est meilleur que nous ne l'espérions, compte tenu du fait que l'équation choisie était la plus simple possible, et aussi que la prédiction s'est faite sans paramètre autre que les constantes λ et εy. Compte tenu aussi de ce que le résultat des expériences et des prédictions est inattendu : ainsi, quand l'obstacle se déplace dans la mousse, même à basse vitesse, l'écoulement de la mousse autour de lui montre une nette asymétrie entre l'amont et l'aval. En outre, derrière l'obstacle, la vitesse de l'écoulement passe par un point d'arrêt, change de signe, augmente, passe par un maximum, et décroît. Or aucun de ces traits caractéristiques n'existe dans un écoulement visqueux simple, visco-élastique ou visco-plastique. Autrement dit, le comportement complexe de la mousse est qualitativement différent des comportements de ses composantes plus simples.
La comparaison de calculs numériques avec des expériences de mousses liquides, présentée au paragraphe précédent, met en évidence l'émergence à grande échelle de propriétés de la mousse qui ne se ramènent pas trivialement aux propriétés des bulles individuelles. Au-dessus de deux ou trois diamètres de bulles, la mousse se comporte comme un milieu continu. Bien que les bulles soient constituées de deux fluides, la mousse est parfois solide, parfois liquide. Mieux même, elle développe les propriétés d'un solide élastique ainsi que celles d'un fluide visco-plastique.
Ce comportement complexe est similaire pour des mousses de composition ou de taille de bulles très différentes. Une telle universalité fait de la mousse un bon système modèle pour comprendre l'originalité de ces matériaux complexes qui sont constitués d'un assemblage de cellules, et plus généralement tous ceux qui sont à la fois visqueux, élastiques et plastiques.
En tout cas, on comprend mieux maintenant pourquoi la mousse, que l'on croirait liquide, reste obstinément coincée par ses propriétés solides dans le goulot de la bouteille où on ne peut l'atteindre !