Les hypothèses
de
modélisation
sont ici plus fortes que dans le
chapitre précédent. Les
données
observées sont vues comme des
réalisations d'un
échantillon
de la
loi normale
![]() ,
dont
l'espérance
,
dont
l'espérance
![]() et la
variance
et la
variance
![]() sont
inconnues. Sous ces hypothèses
des résultats théoriques précisent la
loi des
estimateurs
naturels de
sont
inconnues. Sous ces hypothèses
des résultats théoriques précisent la
loi des
estimateurs
naturels de ![]() et
et ![]() que sont la
moyenne
et la
variance
empiriques.
que sont la
moyenne
et la
variance
empiriques.
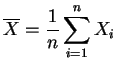 la
moyenne empirique,
la
moyenne empirique,
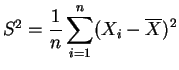 la
variance empirique.
la
variance empirique.
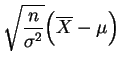 suit la
loi normale
suit la
loi normale
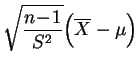 suit la
loi de Student
suit la
loi de Student
Le point 1) permet de tester des
hypothèses
portant sur la valeur de
![]() , quand
, quand ![]() est connu. C'est la situation typique du contrôle
de qualité. Considérons une machine destinée à la fabrication
de comprimés devant peser 1 gramme. Aucun comprimé, s'il est mesuré
au microgramme près, ne pèse 1 gramme exactement. Les poids des
comprimés sont en
moyenne
de 1g, avec un
écart-type
lié aux
caractéristiques de la machine, qui est connu (par exemple
est connu. C'est la situation typique du contrôle
de qualité. Considérons une machine destinée à la fabrication
de comprimés devant peser 1 gramme. Aucun comprimé, s'il est mesuré
au microgramme près, ne pèse 1 gramme exactement. Les poids des
comprimés sont en
moyenne
de 1g, avec un
écart-type
lié aux
caractéristiques de la machine, qui est connu (par exemple
![]() ).
Le contrôle de qualité consistera à prélever périodiquement
un
échantillon
de comprimés dont on calcule le poids moyen pour
tester qu'il ne s'écarte pas trop de la valeur de référence. Par exemple,
si sur un
échantillon
de 10 comprimés on observe un poids moyen
de 0.995, la
statistique de test
prend la valeur
).
Le contrôle de qualité consistera à prélever périodiquement
un
échantillon
de comprimés dont on calcule le poids moyen pour
tester qu'il ne s'écarte pas trop de la valeur de référence. Par exemple,
si sur un
échantillon
de 10 comprimés on observe un poids moyen
de 0.995, la
statistique de test
prend la valeur
![]() , dont la p-valeur
par rapport à la
loi normale
, dont la p-valeur
par rapport à la
loi normale
![]() est :
est :
Si la
variance
est inconnue, on peut utiliser le point 2) de la même
manière. Reprenons les mêmes
données
en supposant que
l'écart-type
de 0.01 a été observé. La
statistique de test
prend la valeur
![]() , dont la
p-valeur
par rapport à la
loi de Student
, dont la
p-valeur
par rapport à la
loi de Student
![]() est :
est :
On peut utiliser le point 3) pour tester la valeur de
l'écart-type.
Toujours sur un échantillon
de 10 comprimés, supposons qu'on ait
observé un
écart-type
de 0.013. On souhaite tester si cette valeur
est significativement trop grande par rapport à la valeur de
référence ![]() 0.01. La
statistique de test
prend la valeur
0.01. La
statistique de test
prend la valeur
![]() . Pour la
loi de chi-deux
. Pour la
loi de chi-deux
![]() , la
p-valeur
correspondante est :
, la
p-valeur
correspondante est :
On fait souvent l'hypothèse de normalité, sans pouvoir toujours la tester valablement. Dans le cas des grands échantillons on peut s'en dispenser, grâce au théorème central limite
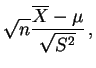
On utilise ce résultat pour tester les valeurs de l'espérance, exactement comme les points 1) et 2) du théorème 3.1.