Comment fait-on pour calculer numériquement une intégrale sur
ordinateur ? Deux cas se présentent, selon que l'on ne connaît
que certaines valeurs de la fonction (typiquement,
par une table de données expérimentales), ou bien que l'on peut
l'évaluer en n'importe quel point. Comme nous allons le voir, la
deuxième situation est beaucoup plus favorable.
Supposons que l'on dispose de 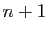 abscisses
abscisses
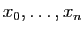 et de
et de 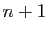 ordonnées
ordonnées
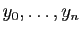 . L'idée la plus naïve est de
calculer la somme des aires de rectangles basés sur les intervalles
. L'idée la plus naïve est de
calculer la somme des aires de rectangles basés sur les intervalles
![$ [x_i,x_{i+1}]$](img633.gif) , et de hauteur
, et de hauteur 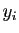 ou bien
ou bien 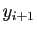 : ce sont les
méthodes des rectangles, à gauche, ou à droite.
: ce sont les
méthodes des rectangles, à gauche, ou à droite.
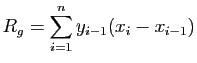
et
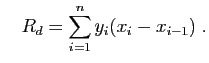
Si on ne sait absolument rien de la fonction à intégrer, il n'y a
pas de raison d'aller plus loin. Mais si on imagine un modèle dans
lequel les ordonnées 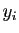 sont les évaluations en
sont les évaluations en 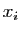 d'une
fonction continue
d'une
fonction continue 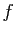 , alors on obtient une meilleure précision par
la méthode des trapèzes, qui consiste simplement à prendre
la demi-somme de
, alors on obtient une meilleure précision par
la méthode des trapèzes, qui consiste simplement à prendre
la demi-somme de 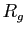 et
et 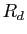 .
.
Si on imagine un modèle où la fonction à intégrer 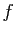 est
encore plus lisse, on gagnera en l'interpolant par une parabole sur
des triplets de points successifs. C'est la méthode de Simpson.
est
encore plus lisse, on gagnera en l'interpolant par une parabole sur
des triplets de points successifs. C'est la méthode de Simpson.
Pour donner une idée de la précision atteinte, supposons que nous
disposions d'une table de 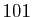 valeurs régulièrement espacées de la
fonction sinus sur l'intervalle
valeurs régulièrement espacées de la
fonction sinus sur l'intervalle ![$ [0,\pi/2]$](img641.gif) . L'intégrale de
. L'intégrale de
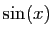 sur
sur ![$ [0,\pi/2]$](img641.gif) vaut
vaut 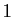 . Voici ce que donnent la méthode
des rectangles à droite et à gauche, la méthode des trapèzes,
et la méthode de Simpson.
. Voici ce que donnent la méthode
des rectangles à droite et à gauche, la méthode des trapèzes,
et la méthode de Simpson.
Quand une fonction est donnée par une expression qui permet de
la calculer en n'importe quel point, il serait particulièrement
inefficace de l'évaluer en 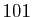 points régulièrement espacés,
pour se ramener au cas précédent.
On utilise plutôt les méthodes de
quadrature de Gauss. Voici comment fonctionne la plus simple, celle de
Gauss-Legendre. Soit une fonction
points régulièrement espacés,
pour se ramener au cas précédent.
On utilise plutôt les méthodes de
quadrature de Gauss. Voici comment fonctionne la plus simple, celle de
Gauss-Legendre. Soit une fonction 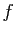 à intégrer sur l'intervalle
à intégrer sur l'intervalle
![$ [a,b]$](img4.gif) . Quitte à effectuer un changement de variable affine, on
peut se ramener au cas où
. Quitte à effectuer un changement de variable affine, on
peut se ramener au cas où 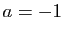 et
et 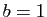 . Les points auxquels on
doit évaluer la fonction sont les racines des polynômes de
Legendre. On peut définir ces polynômes
par récurrence, par une équation différentielle, ou bien comme la
dérivée
. Les points auxquels on
doit évaluer la fonction sont les racines des polynômes de
Legendre. On peut définir ces polynômes
par récurrence, par une équation différentielle, ou bien comme la
dérivée 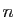 -ième d'un polynôme de degré
-ième d'un polynôme de degré 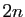 .
.
Les racines de 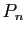 sont dans l'intervalle
sont dans l'intervalle ![$ [-1,1]$](img371.gif) , et réparties de
façon symétrique par rapport à l'origine. Comme
, et réparties de
façon symétrique par rapport à l'origine. Comme 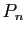 est de
degré
est de
degré 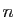 , il a
, il a 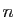 racines : notons-les
racines : notons-les
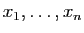 . À la racine
. À la racine
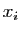 , on associe le «poids»
, on associe le «poids»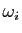 :
:
On calcule ensuite la somme :
Les racines des polynômes de Legendre, ainsi que les poids qui leur
sont associés sont connus depuis longtemps, et
inclus dans les bibliothèques de codes des langages de calcul
scientifique : le calcul de 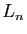 est donc extrêmement rapide. Vous
apprendrez plus tard les raisons mathématiques
pour lesquelles ce calcul donne une valeur approchée précise
de l'intégrale de
est donc extrêmement rapide. Vous
apprendrez plus tard les raisons mathématiques
pour lesquelles ce calcul donne une valeur approchée précise
de l'intégrale de 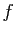 . Les résultats sont spectaculaires. Voici
pour la même fonction sinus entre 0 et
. Les résultats sont spectaculaires. Voici
pour la même fonction sinus entre 0 et 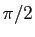 , ce que donne la
méthode de Gauss-Legendre pour
, ce que donne la
méthode de Gauss-Legendre pour
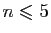 .
.
Ainsi, en évaluant la fonction sinus en 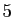 points seulement, on
calcule son intégrale avec une précision de l'ordre de
points seulement, on
calcule son intégrale avec une précision de l'ordre de
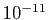 : impressionnant non ?
: impressionnant non ?
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
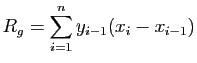 et
et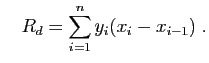
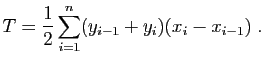
![]() valeurs régulièrement espacées de la
fonction sinus sur l'intervalle
valeurs régulièrement espacées de la
fonction sinus sur l'intervalle ![]() . L'intégrale de
. L'intégrale de
![]() sur
sur ![]() vaut
vaut ![]() . Voici ce que donnent la méthode
des rectangles à droite et à gauche, la méthode des trapèzes,
et la méthode de Simpson.
. Voici ce que donnent la méthode
des rectangles à droite et à gauche, la méthode des trapèzes,
et la méthode de Simpson.
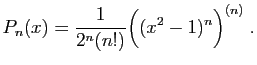
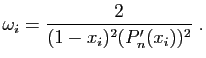
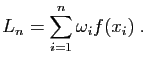
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales