Est-il possible de savoir si une suite converge (vers une limite finie), sans connaître sa limite ? La notion de suite de Cauchy répond à cette question. Elle traduit l'idée intuitive que les termes d'une suite convergente doivent être proches les uns des autres à partir d'un certain rang.
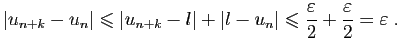
L'intérêt de cette notion est qu'elle caractérise les suites
réelles convergentes : la réciproque du théorème précédent est
vraie dans
![]() .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales