La notion de limite est très liée aux notions de borne supérieure
(plus petit des majorants) et borne inférieure
(plus grand des minorants).
Etant donnée une suite 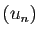 , nous appellerons borne supérieure
et borne inférieure de
, nous appellerons borne supérieure
et borne inférieure de 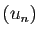 les quantités
les quantités
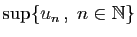
et
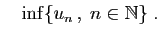
Théorème 2
- Toute suite croissante et majorée converge vers sa borne supérieure.
- Toute suite croissante et non majorée tend vers
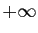 .
.
- Toute suite décroissante et minorée converge vers sa borne inférieure.
- Toute suite décroissante et non minorée tend vers
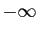 .
.
Démonstration : Rappelons que toute partie non vide et majorée de
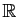 admet une
borne supérieure finie.
Si l'ensemble
admet une
borne supérieure finie.
Si l'ensemble
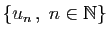 est majoré, il
admet une borne supérieure finie : notons-la
est majoré, il
admet une borne supérieure finie : notons-la 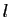 .
Puisque
.
Puisque 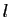 est le plus petit des majorants,
pour tout
est le plus petit des majorants,
pour tout
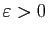 ,
,
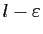 n'est pas un majorant. Donc il existe
n'est pas un majorant. Donc il existe
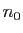 tel que
tel que
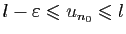 . Mais si
. Mais si 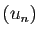 est
croissante, alors pour tout
est
croissante, alors pour tout
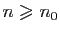 ,
,
donc 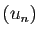 converge vers
converge vers 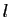 .
.
Si la suite n'est pas majorée, pour tout 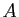 , il existe
, il existe 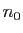 tel
que
tel
que
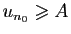 . Si
. Si 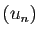 est croissante,
alors pour tout
est croissante,
alors pour tout
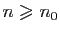 ,
,
donc la suite 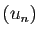 tend vers l'infini.
tend vers l'infini.
Si la suite 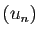 est décroissante, on applique ce qui précède
à la suite croissante
est décroissante, on applique ce qui précède
à la suite croissante 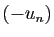 .
. 
Définition 8
Soient 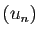 et
et 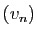 deux suites de réels. Elles sont dites
adjacentes si
deux suites de réels. Elles sont dites
adjacentes si
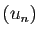 est croissante,
est croissante,
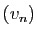 est décroissante,
est décroissante,
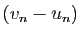 tend vers 0.
tend vers 0.
Proposition 2
Deux suites adjacentes convergent vers la même limite.
Démonstration : Si 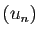 est croissante et
est croissante et 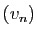 décroissante, alors
décroissante, alors 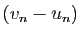 est décroissante. Si
est décroissante. Si 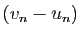 tend vers 0, alors pour tout
tend vers 0, alors pour tout 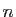 ,
,
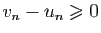 . Donc
. Donc
La suite 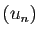 est croissante, et majorée par
est croissante, et majorée par 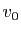 , donc elle converge.
La suite
, donc elle converge.
La suite 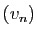 est décroissante, et minorée par
est décroissante, et minorée par 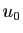 ,
donc elle converge. Comme la différence tend vers 0, les deux
limites sont égales (théorème 1).
,
donc elle converge. Comme la différence tend vers 0, les deux
limites sont égales (théorème 1). Voici un exemple très classique.
Posons :
Voici un exemple très classique.
Posons :
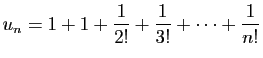
et
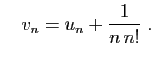
La suite 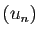 est strictement
croissante car
est strictement
croissante car
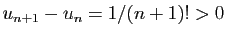 . La suite
. La suite
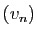 est strictement décroissante :
est strictement décroissante :
La différence 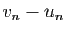 tend vers 0, donc les deux suites convergent vers la
même limite. Cette limite est le nombre
tend vers 0, donc les deux suites convergent vers la
même limite. Cette limite est le nombre
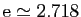 . Les deux suites
fournissent un encadrement extrêmement précis de
. Les deux suites
fournissent un encadrement extrêmement précis de
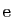 , pour un
nombre de termes calculés relativement faible. Pour
, pour un
nombre de termes calculés relativement faible. Pour 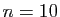 , la
différence
, la
différence 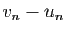 vaut
vaut
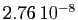 , et pour
, et pour 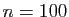 , elle
vaut
, elle
vaut
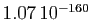 .
.
Ce même encadrement est aussi un moyen de montrer que
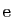 est
irrationnel. Supposons en effet que
est
irrationnel. Supposons en effet que
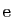 s'écrive
s'écrive
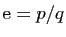 , avec
, avec 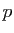 et
et 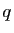 entiers. On aurait
entiers. On aurait
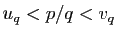 , soit :
, soit :
Multiplions ces inégalités par 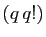 . Le nombre entier
. Le nombre entier
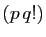 devrait être encadré strictement par deux
entiers consécutifs, ce qui est impossible.
devrait être encadré strictement par deux
entiers consécutifs, ce qui est impossible.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() , nous appellerons borne supérieure
et borne inférieure de
, nous appellerons borne supérieure
et borne inférieure de ![]() les quantités
les quantités
![]() , il existe
, il existe ![]() tel
que
tel
que
![]() . Si
. Si ![]() est croissante,
alors pour tout
est croissante,
alors pour tout
![]() ,
,
![]() est décroissante, on applique ce qui précède
à la suite croissante
est décroissante, on applique ce qui précède
à la suite croissante ![]() .
. ![]()
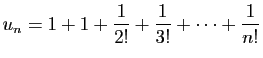 et
et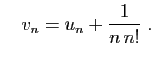
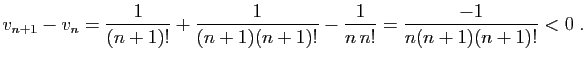
![]() est
irrationnel. Supposons en effet que
est
irrationnel. Supposons en effet que
![]() s'écrive
s'écrive
![]() , avec
, avec ![]() et
et ![]() entiers. On aurait
entiers. On aurait
![]() , soit :
, soit :
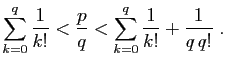
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales