Il n'y a pas beaucoup de séries pour l'instant dont vous connaissiez
la somme, à part la série exponentielle, les séries
géométriques. Il en existe bien d'autres. Voici par exemple deux
résultats classiques, dont vous rencontrerez la justification ailleurs :
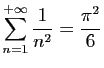
et
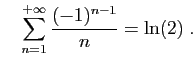
Vous aurez beaucoup plus de techniques à votre disposition après le
chapitre sur les séries entières. En attendant, vous pourrez quand
même calculer certaines sommes, en combinant celles que vous
connaissez. Voici quelques exemples.
Considérons la série
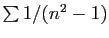 .
C'est bien une série convergente, car son terme général est
positif, et équivalent à
.
C'est bien une série convergente, car son terme général est
positif, et équivalent à
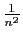 .
Nous allons démontrer que :
.
Nous allons démontrer que :
Utilisons la décomposition en éléments
simples.
Par récurrence, on en déduit l'expression des sommes partielles.
d'où le résultat.
En utilisant la même technique de décomposition en éléments
simples, vous pourrez aussi calculer les sommes suivantes.
Voici maintenant deux exemples de calcul de sommes que l'on ramène
à une série géométrique. Pour le premier, nous revenons sur
les développements décimaux. Si
un nombre 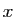 est rationnel, alors son développement décimal,
obtenu en divisant deux entiers, est périodique. Réciproquement,
si le développement décimal d'un réel est périodique, alors ce
réel est un rationnel. Nous allons le calculer. Supposons que
est rationnel, alors son développement décimal,
obtenu en divisant deux entiers, est périodique. Réciproquement,
si le développement décimal d'un réel est périodique, alors ce
réel est un rationnel. Nous allons le calculer. Supposons que
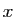 s'écrive :
s'écrive :
Le réel 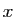 est la somme de la série suivante.
est la somme de la série suivante.
On retrouve la série géométrique 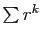 , avec
, avec
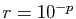 . On en déduit :
. On en déduit :
Soit 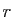 tel que
tel que 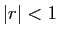 .
Nous allons montrer que
.
Nous allons montrer que
Pour cela écrivons :
d'où le résultat, en résolvant cette équation en 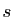 . La
même technique permet de montrer que :
. La
même technique permet de montrer que :
Quand le terme général est le quotient d'un polynôme en 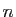 par
par
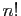 , on peut toujours se ramener à la série exponentielle. Si le
polynôme est
, on peut toujours se ramener à la série exponentielle. Si le
polynôme est 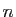 ,
, 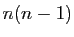 ,..., la simplification est
immédiate.
,..., la simplification est
immédiate.
Un polynôme en 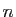 de degré
de degré
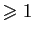 peut toujours s'exprimer
comme combinaison linéaire de
peut toujours s'exprimer
comme combinaison linéaire de 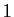 ,
, 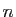 ,
, 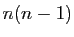 ,... Par exemple,
,... Par exemple,
Vous pourrez procéder de même pour calculer les sommes suivantes.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
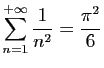 et
et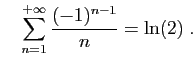
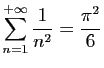 et
et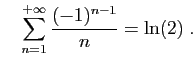
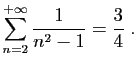
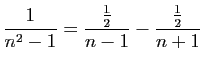
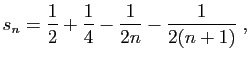
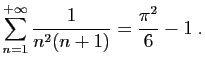
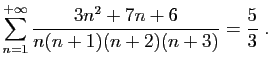
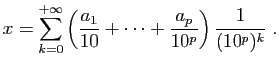
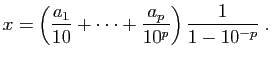
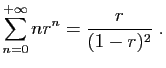
![\begin{displaymath}
\begin{array}{lcl}
s &=&
\displaystyle{ \sum_{n=0}^{+\infty}...
... [2ex]
&=& \displaystyle{ \frac{r}{1-r} +r s\;,}
\end{array}\end{displaymath}](img330.gif)
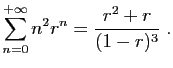
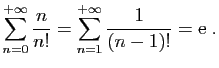
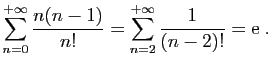
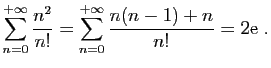
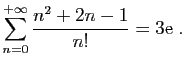
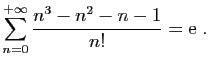
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales