En fait, bien que cette définition soit générale, on
n'aurait pas l'idée
d'appeler «loi de composition» n'importe quelle application
de ![]() vers
vers ![]() ; le
vocable n'est utilisé que quand il est naturel de noter l'application par un
symbole opératoire. Des exemples typiques de lois de composition sont
l'addition
; le
vocable n'est utilisé que quand il est naturel de noter l'application par un
symbole opératoire. Des exemples typiques de lois de composition sont
l'addition ![]() de
de
![]() vers
vers
![]() , qui associe
, qui associe ![]() à
à ![]() ; ou bien
la loi de composition
; ou bien
la loi de composition ![]() sur l'ensemble
sur l'ensemble ![]() des
applications de
des
applications de ![]() vers
vers ![]() , qui associe l'application
, qui associe l'application
![]() au couple d'applications
au couple d'applications ![]() . Pour des lois
de composition abstraites, le
symbole opératoire
. Pour des lois
de composition abstraites, le
symbole opératoire ![]() a été à la mode et nous
l'utiliserons occasionnellement,
surtout au début, mais nous nous contenterons rapidement
de la notation multiplicative
a été à la mode et nous
l'utiliserons occasionnellement,
surtout au début, mais nous nous contenterons rapidement
de la notation multiplicative
![]() , ou même simplement
, ou même simplement ![]() ,
pour l'élément obtenu en appliquant la loi de composition à
,
pour l'élément obtenu en appliquant la loi de composition à ![]() .
.
Voici un peu de vocabulaire au sujet des lois de composition.
La cohérence de ce qui suit nécessite d'énoncer tout de suite un résultat simplissime.
Démonstration : Soit ![]() et
et ![]() deux éléments neutres pour une
loi de composition
deux éléments neutres pour une
loi de composition ![]() .
Comme
.
Comme ![]() est neutre,
est neutre,
![]() et comme
et comme ![]() est neutre,
est neutre,
![]() . Donc
. Donc ![]() .
.![]()
On parlera donc de l'élément neutre avec l'article défini, lorsqu'il existe un élément neutre.
Là encore, glissons sans tarder une évidence.
Démonstration : Soit ![]() le neutre de
le neutre de ![]() , soit
, soit ![]() un
élément de
un
élément de ![]() et soient
et soient ![]() et
et ![]() deux
symétriques de
deux
symétriques de ![]() . Alors d'une
part
. Alors d'une
part
![]() et d'autre part
et d'autre part
![]() . Par associativité
de la loi de composition,
. Par associativité
de la loi de composition,
![]() , d'où
, d'où ![]() .
.![]()
Les lois de composition intéressantes étant en pratique associatives, on pourra donc faire plein usage de la notation suivante.
Maintenant que nous savons manipuler une loi de composition sur un seul ensemble, apprenons à évoluer d'un ensemble muni d'une loi de composition vers un autre.
Il semble plus facile d'expliquer la notion d'isomorphisme que celle de morphisme en général ; deux lois de composition sur deux ensembles fourniront des structures isomorphes lorsque ces deux lois de composition agissent de la même façon, seuls les noms des éléments changeant. La phrase précédente n'étant peut-être pas si claire que cela, donnons plutôt des exemples, c'est toujours bien les exemples.
Pour abréger les calculs qui suivent, introduisons une notation.
En utilisant cette notation, on peut très
facilement calculer tous les produits deux à deux des bijections introduites
ici ; par exemple
![]() .
.
On considère alors l'ensemble
![]() et on voit
que
et on voit
que ![]() est une loi de composition sur ce sous-ensemble de
est une loi de composition sur ce sous-ensemble de ![]() ,
qui sera agréablement décrite par le tableau suivant, que l'on
appelle une table de composition.
,
qui sera agréablement décrite par le tableau suivant, que l'on
appelle une table de composition.

Considérons à présent l'ensemble des nombres complexes dont la
puissance quatrième vaut ![]() , c'est-à-dire l'ensemble
, c'est-à-dire l'ensemble
![]() . Il est très facile de constater que la
multiplication des nombres complexes définit une loi de composition sur
. Il est très facile de constater que la
multiplication des nombres complexes définit une loi de composition sur ![]() ,
dont la table est donnée ci-dessous.
,
dont la table est donnée ci-dessous.
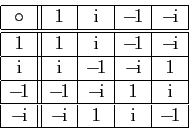
Visuellement, on retrouve la même table, seuls les noms des éléments ont
changé. C'est signe qu'il y a un isomorphisme camouflé. On le détectera
facilement ; c'est bien sûr l'application ![]() de
de ![]() vers
vers ![]() définie par :
définie par :
Il faut tout
d'abord se soucier de vérifier que cette définition n'est pas ambiguë,
car elle n'est pas loin de l'être ! Une rotation peut en effet être
caractérisée par plusieurs angles (tourner d'un quart de tour dans le
sens trigonométrique, c'est aussi tourner de trois quarts de tour dans
le sens des aiguilles d'une montre), mais deux angles distincts
![]() et
et ![]() correspondant à la même bijection diffèrent
d'un multiple entier de
correspondant à la même bijection diffèrent
d'un multiple entier de ![]() ; il existe donc un entier
; il existe donc un entier
![]() tel que
tel que
![]() . Les valeurs
. Les valeurs
![]() et
et
Une fois cette
mise au point effectuée, vérifier que ![]() est un morphisme est
sans problème : si
est un morphisme est
sans problème : si ![]() est la rotation d'angle
est la rotation d'angle ![]() et
et
![]() la rotation d'angle
la rotation d'angle ![]() , la composée
, la composée
![]() est la rotation
est la rotation ![]() d'angle
d'angle
![]() , et on a
donc :
, et on a
donc :
À l'évidence (et c'est sans doute ce que vous
fîtes au lycée), on peut
voir ![]() comme l'application qui «enroule» de façon régulière
une corde (la droite
comme l'application qui «enroule» de façon régulière
une corde (la droite
![]() ) sur une roue (le cercle
) sur une roue (le cercle
![]() ), encore et encore.
), encore et encore.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales