Toutes les matrices considérées sont des matrices carrées
à 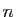 lignes et
lignes et 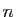 colonnes, à coefficients dans
colonnes, à coefficients dans
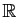 ou
ou
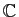 .
Les vecteurs sont identifiés à
des matrices à
.
Les vecteurs sont identifiés à
des matrices à 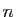 lignes et
lignes et 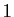 colonne.
colonne.
Une matrice
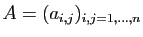 est diagonale si tous ses coefficients en
dehors de la diagonale sont nuls.
est diagonale si tous ses coefficients en
dehors de la diagonale sont nuls.
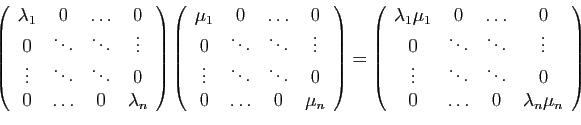
Elle est donc de la forme :
Pour comprendre le rôle des coefficients diagonaux, supposons tout
d'abord qu'ils sont tous égaux à 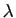 . Dans ce cas,
. Dans ce cas,
 est proportionnelle à la matrice identité :
est proportionnelle à la matrice identité :
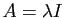 . Pour tout vecteur
. Pour tout vecteur 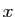 de
de
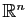 , le vecteur
, le vecteur 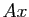 est
proportionnel à
est
proportionnel à 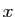 :
:
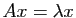 . Multiplier le vecteur
. Multiplier le vecteur 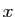 par la matrice
par la matrice  revient à le multiplier par le facteur
revient à le multiplier par le facteur
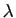 . Géométriquement, c'est effectuer une homothétie
de rapport
. Géométriquement, c'est effectuer une homothétie
de rapport 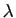 .
Supposons maintenant que les coefficients diagonaux soient
quelconques. Considérons une base
.
Supposons maintenant que les coefficients diagonaux soient
quelconques. Considérons une base
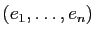 de
de
 , et
examinons l'endomorphisme
, et
examinons l'endomorphisme 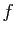 de
de
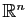 , de matrice
, de matrice  dans cette
base. Dire que
dans cette
base. Dire que
 est diagonale, c'est dire que l'image du vecteur
est diagonale, c'est dire que l'image du vecteur 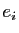 de la base
est
de la base
est
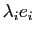 . Si on restreint
. Si on restreint 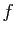 à la direction
à la direction 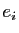 ,
, 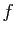 est une homothétie de rapport
est une homothétie de rapport 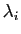 . Si
. Si 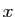 est un vecteur
quelconque de
est un vecteur
quelconque de
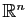 ,
, 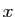 s'écrit
s'écrit
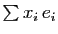 . Son image par
. Son image par
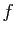 est :
est :
Les matrices diagonales sont
particulièrement simples à manipuler. Voici les propriétés
principales :
- Le déterminant d'une matrice diagonale est le produit des
coefficients diagonaux.
- Multiplier à gauche par une matrice diagonale revient à multiplier
la
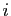 -ième ligne par
-ième ligne par 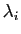 : si
: si
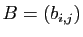 est une matrice
quelconque, alors
est une matrice
quelconque, alors
- Multiplier à droite par une matrice diagonale revient à multiplier
la
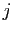 -ième colonne par
-ième colonne par 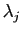 : si
: si
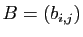 est une matrice
quelconque, alors
est une matrice
quelconque, alors
- Le produit de deux matrices diagonales est une matrice diagonale.
- Si tous les coefficients diagonaux sont non nuls, la matrice est
inversible :
- La puissance
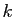 -ième d'une matrice diagonale est :
-ième d'une matrice diagonale est :
Pour une matrice  quelconque, les calculs se simplifient à partir
du moment où elle est semblable à une matrice diagonale.
Deux matrices
quelconque, les calculs se simplifient à partir
du moment où elle est semblable à une matrice diagonale.
Deux matrices  et
et 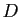 sont
semblables, lorsqu'elles représentent le même endomorphisme dans deux bases
différentes, ou encore, quand il existe une matrice de passage
sont
semblables, lorsqu'elles représentent le même endomorphisme dans deux bases
différentes, ou encore, quand il existe une matrice de passage 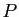 telle que
telle que
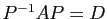 . Par exemple :
. Par exemple :
Définition 1
Une matrice  est dite diagonalisable si elle est semblable à une
matrice diagonale.
est dite diagonalisable si elle est semblable à une
matrice diagonale.
L'objectif des deux premières sections de ce chapitre
est d'apprendre à diagonaliser une
matrice, quand c'est possible.
Définition 2
Diagonaliser une matrice  , c'est trouver une matrice de
passage
, c'est trouver une matrice de
passage 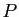 et une matrice diagonale
et une matrice diagonale 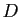 telles que :
telles que :
Si
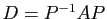 , alors
, alors
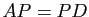 . Mais si
. Mais si 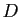 est une matrice diagonale, multiplier
est une matrice diagonale, multiplier 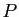 à
droite par
à
droite par 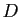 revient à multiplier les vecteurs colonnes de
revient à multiplier les vecteurs colonnes de 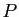 par
les coefficients diagonaux de
par
les coefficients diagonaux de 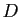 . Notons
. Notons 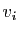 le
le 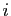 -ième vecteur
colonne de la matrice
-ième vecteur
colonne de la matrice 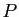 et
et 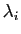 le
le 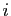 -ième coefficient
diagonal de
-ième coefficient
diagonal de 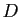 . Pour tout
. Pour tout
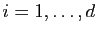 , on doit avoir :
, on doit avoir :
en notant 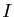 la matrice identité de dimension
la matrice identité de dimension 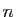 .
On dit que
.
On dit que 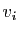 est un vecteur propre de
est un vecteur propre de  associé à la
valeur propre
associé à la
valeur propre 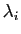 .
.
Observons que 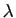 est une valeur propre de
est une valeur propre de  si et seulement si
le système
si et seulement si
le système
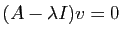 a une solution non nulle.
Voici deux manières
équivalentes de l'exprimer.
a une solution non nulle.
Voici deux manières
équivalentes de l'exprimer.
Définition 4
On appelle polynôme caractéristique de la matrice  , et
on note
, et
on note 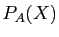 le déterminant de la matrice
le déterminant de la matrice 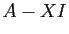 .
.
D'après la forme développée d'un déterminant, 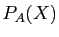 est une
somme de produits des termes de la matrice.
Chaque produit est constitué de
est une
somme de produits des termes de la matrice.
Chaque produit est constitué de 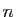 facteurs qui
sont des termes pris dans des lignes et des colonnes
différentes. Le terme de plus haut degré en
facteurs qui
sont des termes pris dans des lignes et des colonnes
différentes. Le terme de plus haut degré en 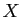 dans le
déterminant
dans le
déterminant 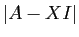 provient du produit des termes qui
contiennent tous
provient du produit des termes qui
contiennent tous 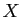 , à savoir les coefficients diagonaux :
, à savoir les coefficients diagonaux :
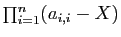 .
Le polynôme caractéristique
.
Le polynôme caractéristique 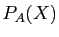 est donc de degré
est donc de degré 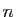 : son terme de plus
haut degré est
: son terme de plus
haut degré est 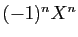 .
Tant que nous y sommes, observons que le terme constant de
.
Tant que nous y sommes, observons que le terme constant de
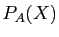 est le déterminant de
est le déterminant de  ; c'est aussi le produit
des valeurs propres (comptées avec leurs multiplicités). Le
coefficient du terme de degré
; c'est aussi le produit
des valeurs propres (comptées avec leurs multiplicités). Le
coefficient du terme de degré 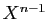 dans
dans 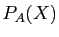 est la somme
des termes diagonaux, que l'on appelle la trace de la matrice
est la somme
des termes diagonaux, que l'on appelle la trace de la matrice
 ; c'est aussi la somme des valeurs propres (toujours
comptées avec leurs multiplicités).
Comme les valeurs propres sont
racines du polynôme caractéristique, une
matrice de dimensions
; c'est aussi la somme des valeurs propres (toujours
comptées avec leurs multiplicités).
Comme les valeurs propres sont
racines du polynôme caractéristique, une
matrice de dimensions 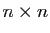 admet au plus
admet au plus 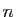 valeurs propres
distinctes.
Pour qu'une matrice soit diagonalisable, il faut déjà que son polynôme
caractéristique admette effectivement
valeurs propres
distinctes.
Pour qu'une matrice soit diagonalisable, il faut déjà que son polynôme
caractéristique admette effectivement 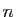 racines (comptées avec
leurs ordres de multiplicité), donc qu'il soit
scindé. C'est toujours le cas dans
racines (comptées avec
leurs ordres de multiplicité), donc qu'il soit
scindé. C'est toujours le cas dans
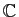 , pas toujours dans
, pas toujours dans
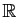 .
Si
.
Si 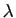 est une valeur propre, l'ensemble des vecteurs
est une valeur propre, l'ensemble des vecteurs 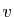 tels
que
tels
que
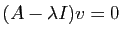 , est un sous-espace vectoriel. Par
définition, il contient le vecteur nul, et tous les
vecteurs propres de
, est un sous-espace vectoriel. Par
définition, il contient le vecteur nul, et tous les
vecteurs propres de  associés à
associés à
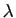 . On l'appelle le «sous-espace propre» associé à
. On l'appelle le «sous-espace propre» associé à
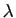 .
.
Définition 5
Soit 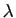 une valeur propre, on appelle sous-espace propre
associé à
une valeur propre, on appelle sous-espace propre
associé à 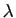 l'espace vectoriel
l'espace vectoriel
Démonstration : Remarquons qu'un même vecteur propre ne peut être
associé qu'à une seule valeur propre. Par conséquent,
deux sous-espaces propres associés à deux valeurs
propres distinctes ont une intersection
réduite au vecteur nul : les sous-espaces propres sont en
somme directe.
Supposons que  soit diagonalisable :
soit diagonalisable :
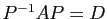 , mais aussi
, mais aussi
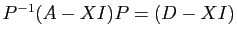 . Les propriétés générales des
déterminants font que
. Les propriétés générales des
déterminants font que
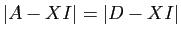 : le polynôme
caractéristique de
: le polynôme
caractéristique de  et celui de
et celui de 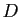 sont les mêmes :
sont les mêmes :
Or le polynôme caractéristique de 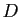 est le produit des termes
diagonaux. Cela signifie que pour tout
est le produit des termes
diagonaux. Cela signifie que pour tout
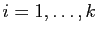 , exactement
, exactement
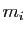 termes diagonaux de
termes diagonaux de 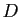 sont égaux à
sont égaux à 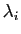 .
Il existe donc
.
Il existe donc 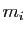 vecteurs colonnes de
vecteurs colonnes de 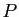 qui sont
des vecteurs propres de
qui sont
des vecteurs propres de  , associés à la valeur propre
, associés à la valeur propre
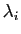 . Comme ces vecteurs forment une famille libre,
la dimension du sous-espace propre associé est au moins égale à
. Comme ces vecteurs forment une famille libre,
la dimension du sous-espace propre associé est au moins égale à
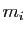 . Comme
. Comme
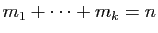 , et que les
sous-espaces propres sont en somme directe, chacun est de
dimension exactement
, et que les
sous-espaces propres sont en somme directe, chacun est de
dimension exactement 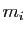 et leur somme directe est
et leur somme directe est
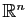 .
Réciproquement, si pour tout
.
Réciproquement, si pour tout 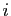 le sous-espace propre associé à
le sous-espace propre associé à
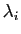 est de dimension
est de dimension 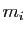 , alors leur somme directe est
, alors leur somme directe est
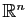 : on peut constituer une base de
: on peut constituer une base de
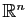 en choisissant une
base de vecteurs dans chaque sous-espace propre.
en choisissant une
base de vecteurs dans chaque sous-espace propre. La mauvaise nouvelle est que toutes les matrices ne sont pas
diagonalisables. La bonne nouvelle est que celles que vous
rencontrerez, entreront souvent dans l'une des catégories
couvertes par les deux théorèmes suivants : valeurs propres toutes
distinctes, ou bien matrices symétriques.
La mauvaise nouvelle est que toutes les matrices ne sont pas
diagonalisables. La bonne nouvelle est que celles que vous
rencontrerez, entreront souvent dans l'une des catégories
couvertes par les deux théorèmes suivants : valeurs propres toutes
distinctes, ou bien matrices symétriques.
Théorème 2
Soit  une matrice admettant
une matrice admettant 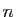 valeurs propres toutes distinctes. Alors
valeurs propres toutes distinctes. Alors  est diagonalisable.
est diagonalisable.
Démonstration : Nous allons montrer par récurrence sur 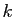 que si
que si
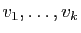 sont des vecteurs propres associés à des valeurs propres
sont des vecteurs propres associés à des valeurs propres
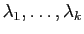 toutes distinctes, alors
toutes distinctes, alors
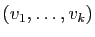 est une famille libre :
est une famille libre :
C'est vrai pour  , puisque par définition un vecteur propre est
non nul. Supposons la propriété vraie à l'ordre
, puisque par définition un vecteur propre est
non nul. Supposons la propriété vraie à l'ordre
 . Soient
. Soient
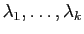 des valeurs propres
distinctes deux à deux et
des valeurs propres
distinctes deux à deux et
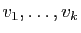 des vecteurs propres
associés. Supposons :
des vecteurs propres
associés. Supposons :
En multipliant à gauche par la matrice  , on obtient :
, on obtient :
Mais aussi :
Soit en soustrayant les deux équations :
D'après l'hypothèse de récurrence à l'ordre 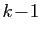 , ceci
entraîne que pour tout
, ceci
entraîne que pour tout
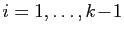 ,
,
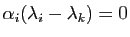 , donc
, donc
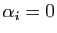 , puisque
, puisque
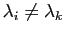 . Mais alors nécessairement
. Mais alors nécessairement
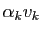 est nul, donc
est nul, donc
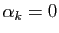 puisque le vecteur propre
puisque le vecteur propre 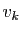 est non
nul.
Supposons qu'une matrice
est non
nul.
Supposons qu'une matrice  admette
admette 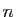 valeurs propres toutes distinctes
valeurs propres toutes distinctes
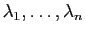 . Pour
. Pour
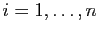 , choisissons un
vecteur propre
, choisissons un
vecteur propre 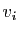 associé à
associé à 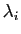 . D'après ce qui précède
. D'après ce qui précède
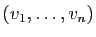 est une famille libre de
est une famille libre de
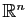 , donc une base.
, donc une base.
Théorème 3
Soit
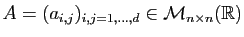 une matrice symétrique :
une matrice symétrique : 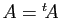 . Alors :
. Alors :
- toutes les valeurs
propres de
 sont réelles ;
sont réelles ;
 est diagonalisable ;
est diagonalisable ;
- on peut choisir comme base de vecteurs propres une base
telle que la matrice de passage
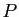 vérifie
vérifie
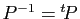 (une
telle base est dite orthonormée).
(une
telle base est dite orthonormée).
Le fait d'avoir une base orthonormée permet d'écrire l'inverse de
la matrice de passage sans calcul supplémentaire (car
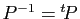 ). Ce théorème est un cas particulier d'un résultat plus
général, pour une matrice
). Ce théorème est un cas particulier d'un résultat plus
général, pour une matrice  à valeurs
complexes qui est hermitienne, c'est-à-dire telle que
à valeurs
complexes qui est hermitienne, c'est-à-dire telle que
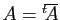 , soit
, soit
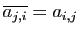 , où
, où
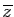 désigne le conjugué du nombre
complexe
désigne le conjugué du nombre
complexe 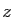 . Les valeurs propres d'une matrice hermitienne
sont réelles, la
matrice est diagonalisable et
il existe une matrice de vecteurs propres unitaire, à savoir
telle que
. Les valeurs propres d'une matrice hermitienne
sont réelles, la
matrice est diagonalisable et
il existe une matrice de vecteurs propres unitaire, à savoir
telle que
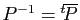 .
Démonstration : Soit
.
Démonstration : Soit 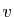 un vecteur non nul de
un vecteur non nul de
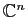 . Considérons le produit :
. Considérons le produit :
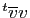 . C'est la somme des modules des coordonnées de
. C'est la somme des modules des coordonnées de
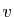 , à savoir un réel strictement positif.
Soit
, à savoir un réel strictement positif.
Soit 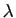 une racine (dans
une racine (dans
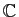 ) de
) de 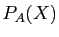 , et soit
, et soit 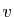 un vecteur propre associé à la valeur propre
un vecteur propre associé à la valeur propre
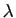 . Donc :
. Donc :
Prenons le conjugué de la transposée de ce même produit
(rappelons que
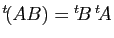 ).
).
puisque  est symétrique. Donc
est symétrique. Donc
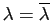 : la valeur propre
: la valeur propre 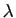 est
réelle.
Considérons l'ensemble des vecteurs orthogonaux à
est
réelle.
Considérons l'ensemble des vecteurs orthogonaux à 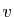 :
:
L'ensemble 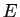 est le noyau d'une application linéaire de rang
est le noyau d'une application linéaire de rang 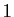 (car
(car 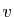 est non nul). C'est donc un sous-espace vectoriel de
est non nul). C'est donc un sous-espace vectoriel de
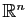 ,
de dimension
,
de dimension 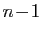 . Soit
. Soit 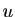 un vecteur de
un vecteur de 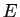 :
:
Donc 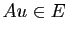 (on dit que
(on dit que 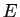 est stable par
est stable par  ).
Nous admettrons ici que dans tout espace vectoriel de dimension finie, il
est possible de choisir une base orthormale (par exemple
grâce au procédé d'orthogonalisation de Gram-Schmidt, vu dans un
autre chapitre).
Soit
).
Nous admettrons ici que dans tout espace vectoriel de dimension finie, il
est possible de choisir une base orthormale (par exemple
grâce au procédé d'orthogonalisation de Gram-Schmidt, vu dans un
autre chapitre).
Soit
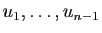 une base orthonormale de
une base orthonormale de 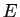 .
Quitte à diviser
.
Quitte à diviser 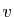 par
par
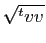 ,
on peut supposer que
,
on peut supposer que 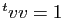 . Par construction,
. Par construction,
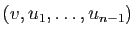 est donc une base orthonormale de
est donc une base orthonormale de
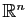 . Notons
. Notons 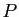 la
matrice de ses vecteurs colonnes :
la
matrice de ses vecteurs colonnes :
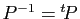 . Au travers du
changement de base de matrice de passage
. Au travers du
changement de base de matrice de passage 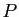 ,
,  est transformée en
une matrice diagonale par blocs :
est transformée en
une matrice diagonale par blocs :
En effet, la première colonne est nulle après le premier terme car
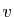 est un vecteur propre associé à
est un vecteur propre associé à 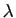 . La première ligne
est nulle après le premier terme car
. La première ligne
est nulle après le premier terme car 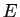 est stable par
est stable par  : les
images de
: les
images de
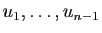 appartiennent à
appartiennent à 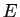 .
De plus :
.
De plus :
de sorte que
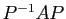 est symétrique, donc
est symétrique, donc  l'est aussi. D'où le
résultat, par récurrence sur
l'est aussi. D'où le
résultat, par récurrence sur  .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() est diagonale si tous ses coefficients en
dehors de la diagonale sont nuls.
est diagonale si tous ses coefficients en
dehors de la diagonale sont nuls.

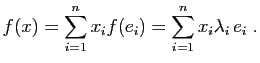
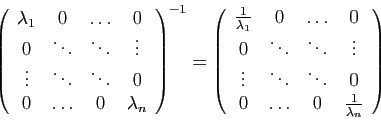
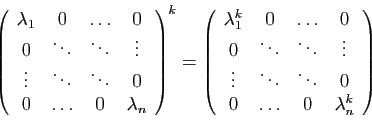
![\begin{displaymath}
\stackrel{
\underbrace{
\left(
\begin{array}{rrr}
\frac{1}{2...
...& 0 [2ex]
0&-1& 0 [2ex]
0&0& 2
\end{array}\right)
}}{D}
\end{displaymath}](img39.gif)
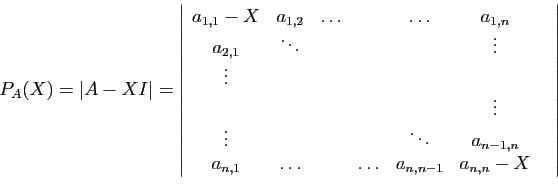
![]() soit diagonalisable :
soit diagonalisable :
![]() , mais aussi
, mais aussi
![]() . Les propriétés générales des
déterminants font que
. Les propriétés générales des
déterminants font que
![]() : le polynôme
caractéristique de
: le polynôme
caractéristique de ![]() et celui de
et celui de ![]() sont les mêmes :
sont les mêmes :
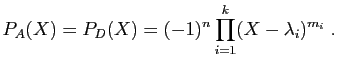
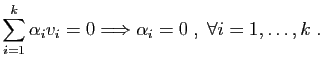
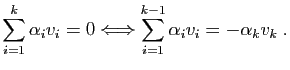
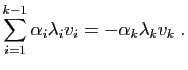
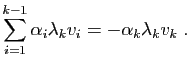
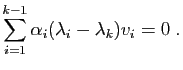
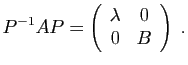
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales