Essayez de bien rédiger vos réponses, sans vous
reporter ni au cours, ni au corrigé.
Si vous souhaitez vous évaluer, donnez-vous deux heures ; puis comparez
vos réponses avec le corrigé et comptez un point pour
chaque question à laquelle vous aurez correctement répondu.
Questions de cours :
Soit 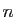 un entier supérieur ou égal à
un entier supérieur ou égal à 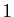 ,
,
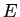 un espace vectoriel de dimension
un espace vectoriel de dimension 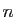 et
et 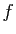 un endomorphisme
de
un endomorphisme
de 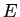 .
.
- Donner la définition du polynôme caractéristique de
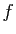 et
énoncer le théorème de Cayley-Hamilton.
et
énoncer le théorème de Cayley-Hamilton.
- Donner la
définition du polynôme minimal de
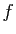 .
.
- On suppose que le polynôme caractéristique est scindé. On
note
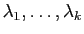 ses racines et
ses racines et
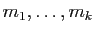 leurs multiplicités respectives.
Montrer que le polynôme minimal de
leurs multiplicités respectives.
Montrer que le polynôme minimal de 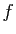 s'écrit
s'écrit
où pour tout
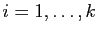 ,
,
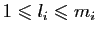 .
.
- Montrer que si
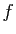 est diagonalisable, alors
est diagonalisable, alors
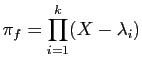 .
.
- Montrer que si
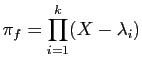 alors
alors 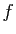 est diagonalisable.
est diagonalisable.
Exercice 1 :
Soit 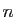 un entier supérieur ou égal à
un entier supérieur ou égal à 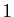 . On note
. On note 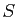 la
matrice de taille
la
matrice de taille
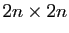 dont le coefficient d'ordre
dont le coefficient d'ordre 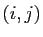 vaut
vaut 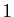 si
si 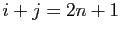 et 0 sinon.
et 0 sinon.
- Vérifier que
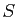 est symétrique, en déduire qu'elle est diagonalisable.
est symétrique, en déduire qu'elle est diagonalisable.
- Montrer que
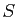 est son propre inverse.
est son propre inverse.
- En déduire le polynôme minimal de
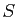 .
.
- Pour tout
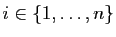 , on note
, on note 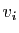 et
et 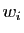 les vecteurs
de
les vecteurs
de
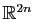 définis par :
définis par :
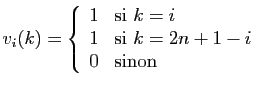
et
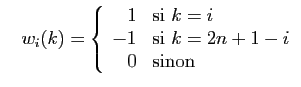
Montrer que 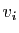 et
et 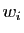 sont vecteurs propres de
sont vecteurs propres de 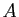 , associés
respectivement aux valeurs propres
, associés
respectivement aux valeurs propres 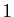 et
et 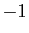 .
.
- Soit
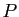 la matrice dont les vecteurs colonnes sont
la matrice dont les vecteurs colonnes sont
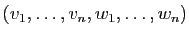 . Montrer que
. Montrer que
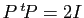 .
.
- En déduire une diagonalisation de
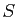 dans une base orthonormée.
dans une base orthonormée.
- Soient
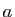 et
et 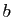 deux réels. On pose
deux réels. On pose 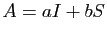 , où
, où 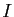 désigne
la matrice identité de taille
désigne
la matrice identité de taille
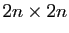 .
Diagonaliser
.
Diagonaliser 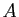 dans une base orthonormée. Quel est le polynôme
caractéristique de
dans une base orthonormée. Quel est le polynôme
caractéristique de 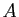 ? Quel est son polynôme minimal ?
? Quel est son polynôme minimal ?
Exercice 2 :
Soient 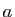 ,
, 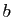 ,
, 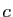 ,
, 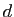 quatre réels tels que
quatre réels tels que 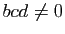 . On
définit la matrice
. On
définit la matrice 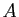 par :
par :
- Calculer
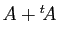 ,
,
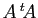 , puis
, puis
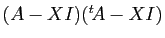 .
.
- En déduire le polynôme caractéristique de
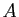 .
.
- Montrer que
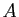 n'est pas diagonalisable sur
n'est pas diagonalisable sur
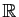 .
.
- Calculer
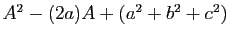 . En déduire le polynôme
minimal de
. En déduire le polynôme
minimal de 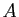 . Montrer que
. Montrer que 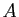 est
diagonalisable sur
est
diagonalisable sur
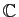 .
.
- On se place désormais dans le cas où
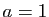 ,
, 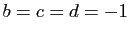 . Vérifier
que
. Vérifier
que
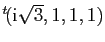 et
et
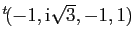 sont des vecteurs propres de
sont des vecteurs propres de 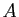 .
.
- En déduire une matrice de passage
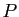 et une matrice diagonale
et une matrice diagonale 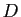 telles que
telles que
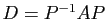 .
.
- Montrer que
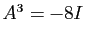 . Pour tout
. Pour tout
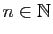 ,
donner l'expression de
,
donner l'expression de 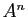 en fonction de
en fonction de 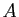 et
et 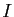 .
.
- Soit
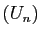 la suite définie par
la suite définie par
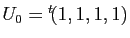 , et pour
tout
, et pour
tout
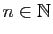 ,
,
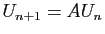 .
Donner l'expression de
.
Donner l'expression de 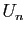 en fonction de
en fonction de 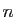 .
.
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales
![]() un entier supérieur ou égal à
un entier supérieur ou égal à ![]() ,
,
![]() un espace vectoriel de dimension
un espace vectoriel de dimension ![]() et
et ![]() un endomorphisme
de
un endomorphisme
de ![]() .
.
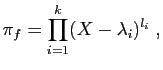
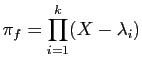 .
.
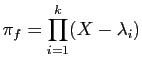 alors
alors 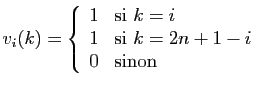 et
et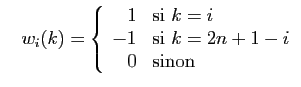
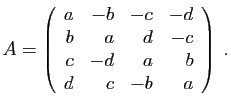
 © UJF Grenoble, 2011
Mentions légales
© UJF Grenoble, 2011
Mentions légales